John Freebairn is a Professor in the Department of Economics at The University of Melbourne, Parkville, Victoria.

Ellen Goddard is a Professor in the Department of Rural Economy at the University of Alberta , Edmonton, Alberta, Canada.

Garry Griffith is a Principal Research Scientist with the NSW Department of Primary Industries, Armidale, New South Wales and an Adjunct professor in the School of Economics at the University of New England, Armidale, New South Wales.

The authors wish to acknowledge the financial assistance of the Rural Industries Research and Development Corporation and the support and constructive comments of Jeff Davis, and the helpful comments of an anonymous referee on an earlier draft.

Abstract

Generic advertising has been a widely-used marketing tool of many agricultural industries. The strategy has come under increasing scrutiny lately, especially by levy-paying producers who fund the advertising. Also, for many food products, supermarket chains have developed and advertised their own “store” or “private label” brands in competition with both processor brands and generic advertising of those products. In such an environment, the issue is whether generic promotion will increase producer returns? Farmers gain from a generic advertising program only if the net farm price rises, where the net farm price is inclusive of the levy collected to fund the generic advertising program. A higher net price to farmers increases producer surplus, or the returns on farmer-owned land, management, labour and other resources which are in limited supply. The aim of this research is to examine the conditions under which such an increase in the net farm price is likely to occur. In undertaking this task, two main areas of research are reported. First, the literature is reviewed and theoretical models are developed to assess the conditions under which farmers would gain from a generic advertising program funded by a levy on production. Second, a general model is applied across the range of Australian agricultural products to assess the minimum increase in domestic sales from advertising required if the program is to increase farmer returns. In particular, the assessment distinguishes products by their exposure to international trade.

Keywords: generic advertising, farmer returns, per unit levy, breakeven analysis, international trade

1. Introduction

Generic advertising to increase the demand for agricultural products has been used as one way of raising farm returns. It has to compete for funds which otherwise might be invested in on-farm expenditures on machinery, land improvement and so forth or into R&D programs. Like any other expenditure, a generic advertising program is of value to farmers only if the marginal returns to them exceed the marginal costs.

Most generic advertising programs are directed at increasing retail demand of the domestic product. In some cases the advertising may be directed at export sales, or to both domestic and export sales, or even to sales to processors lower down the supply chain. Generic advertising can increase sales by providing information, for example on prices and product availability and on nutrition, or by seeking to change consumer preferences in favour of the advertised product, for example healthy lifestyles and happy, energetic consumers. In the end, farmers potentially gain when the increase in retail demand results in an increase in the derived demand for the farm product.

The levy to fund the generic advertising program also is a cost to farmers. Typically it will be a fee per unit of physical market sales or an ad valorem charge as a percentage of farm sales. In both cases the levy effectively is a variable cost which raises marginal farm supply cost. In special cases the levy may be more like a fixed cost that does not vary with output, for example a charge per farm or carry-over funds from previous years. Generic advertising programs often are supported by legislation to ensure that all farmers contribute their share to the advertising program and to prevent free riding.

Evaluation of the net benefits to farmers of a generic advertising program needs to be cognisant of the important characteristics of the industry and the advertising program. The many farmers producing similar products mean that the farm sector is a competitive industry, where individual farmers accept the market price as their marginal return for extra production. The advertising program has to be evaluated in a context of no supply control, in the sense that if the farm price rises, farmers will respond by increasing production. By contrast, brand advertising, and much of the marketing literature on advertising, considers the case where individual firms have some market power and they control supply. A generic advertising program can increase farmer returns (and here we refer to the return on their land, labour, management and other resources whose supply is fixed, or what in economics is called “producer surplus”), only if the program raises the farm price.

Our broad research question therefore is to investigate the conditions under which a generic advertising program can increase farmer returns.

2. Objectives and Outline

Since a generic advertising program funded by a levy shifts outwards the retail demand curve and raises farm costs, we need to model the effects of these demand curve changes and cost changes on market prices and quantities, and in particular on the net farm return. Standard partial equilibrium models of agricultural product markets are used to assess the comparative price and quantity equilibrium effects of the program.

However, our knowledge of the magnitude of the effect of generic advertising programs on the shift in the demand for agricultural products is unsatisfactory at best. In about a half of the reported econometric studies of one product subgroup (reviewed later in Table 3), no statistically significant effect was found. In many studies where a significant effect has been found, the estimated effect has wide sampling errors. Often the data are not adequate, and there are the usual reservations about model specification and appropriate estimation procedures. Anecdotal evidence suggests that the quality and effectiveness of brand and generic advertising programs is variable. Rather than use contentious estimates of the response of sales to generic advertising, this research has adopted a more conservative strategy to assess whether a generic advertising program can increase farmer returns; and then to derive the minimum increase in sales which would need to be induced by a generic advertising program funded by a levy, for farmers to gain. This then provides a benchmark for assessing program proposals and for negotiating with advertising agencies.

As a by-product of the analysis, the paper also derives expressions for the advertising intensity which would maximise returns to farmers. This level is where the marginal benefits equal the marginal costs.

The following section provides a review of the literature and some model development. Most of the focus is on generic advertising funded by a production levy, with brief overviews for programs funded by a lump sum and for brand advertising programs. The section begins with a basic model which assumes competitive behaviour in the post-farm as well as the farm sector, which ignores advertising reactions, and which assumes a constant rate of transformation of the farm product to the retail products. The effects of relaxing each of these simplifying assumptions on the derived minimum advertising responses and profit maximising advertising intensities is then assessed. In the analysis, special attention is given to the trade status of the market, with particular cases of a non-traded product, a small country exporter and a large country exporter.

The material in Section 3 covers a lot of economic concepts. Readers without an interest in the technical detail could go straight to Section 4, which applies the benchmark or minimum-required advertising response models to a range of Australian agricultural products. The minimum increase in domestic sales from the generic advertising program for farmers to gain are derived for different levels of the levy, different degrees of importance of exports in total sales, and for different values of the own-price elasticities of domestic demand and export demand. Then three groups of products are crudely allocated to different parameter combinations.

The paper concludes with a summary of the main results, implications and areas for further research.

3. Advertising Models and the Literature

3.1 Introduction

This section reviews some of the models reported in the literature for evaluating the benefits to farmers from generic advertising programs. The effects of advertising have been evaluated in many articles for a wide range of situations and assumptions in the marketing, industrial organisation, agricultural economics and other literatures. Our principal interest is in those situations with a competitive farm supply in which individual farmers are free to choose production levels at the point where their marginal cost (including the opportunity costs of all resources) equals the farm price net of the levy. This rules out much of the literature on brand advertising where the advertiser also is able to restrict quantity supplied; but for completeness, we include a short section on brand advertising. Most of our literature review focuses on generic advertising programs funded by a levy on farmers (either a per unit of output levy or an ad valorem levy). Again for completeness, we include some brief comments on models of advertising funded by a lump sum mechanism which does not alter the farm product supply curve.

Even when restricted to generic advertising programs without supply control funded by a levy on production, there are many important model variations. With respect to trade status, there are variants for non-traded, or export or import products, and then within the traded-products group, whether Australian trade affects the world price. Another dimension is the form of and the extent of the exercise of market power by processors, wholesalers and retailers involved in transforming farm products into retail products purchased by households. Such market power can be either monopoly power against buyers, or monopsony power against input suppliers, or both. Different results on the returns to farmers from advertising also arise from the assumed production technology affecting the transformation of farm products into retail products (from the simplest assumption of a constant transformation ratio to a more general model that allows for substitution of farm and non-farm inputs in response to changes in relative input costs). Finally, different reactions in the levels of brand advertising by processors and retailers to changes in the generic advertising program also alter the effects on farmer returns from a generic advertising program. Importantly, different patterns of assumptions better fit different Australian agricultural products.

The over-riding condition is that a generic advertising program increases farm returns only if the program results in a net increase in the farm price received. This price increase becomes an increase in the quasi-rent, or “producer surplus”, earned by farmer-owned land, management and other inputs in limited supply. Then, minimum or necessary conditions for a generic advertising program to improve farmer returns are that:

• The advertising program increases the quantity demanded;
• The farm level demand curve is less than perfectly elastic, so that the demand shift leads to a price rise; and
• The farm level supply curve is less than perfectly elastic, so that the demand shift leads to a price rise.

Thus, if the product is internationally traded, either as an exported product or as an imported product, if the domestic and world products are perfect substitutes, and if Australia is a small country in the sense that changes in our international trade has no effect on the world price, then advertising will not raise the farm price. Or, if the farm supply curve is perfectly elastic because there are no fixed factors of production and therefore no quasi-rents, advertising will not raise the farm price.

Section 3.2 considers the literature and theoretical models for generic advertising programs funded by a levy on farm production. The case where the funds can be considered as a lump sum charge is covered in Section 3.3, and particularly the contrasting outcomes for levy versus lump sum funding. Section 3.4 briefly considers brand advertising where firms have control over the quantity supplied as well as advertising. Section 3.5 considers two questions on the advertising response function, namely time of effects and the functional form. A final section provides some conclusions.

3.2 Generic Advertising Funded by a Levy

Section 3.2.1 presents a simple model to illustrate the key points. A more formal model to derive formulae for the effects of advertising for a competitive model with no international trade is given in section 3.2.2. Section 3.2.3 generalises the non-traded product model to allow for international trade. Returning to the non-traded model, the effects of different models of market power in the post-farm sector on farmer returns are discussed in section 3.2.4. Section 3.2.5 considers the direction of effects on returns to farmers if the farmer-funded generic advertising program induces changes in other advertising programs funded by processors or retailers. Alternative model assumptions about the technology available for transforming the farm product and non-farm inputs into the retail product on the measured returns to farmers of advertising are discussed in section 3.2.6.

3.2.1 Basic Story

A simple partial equilibrium model of the demand for and supply of product at the farm level is used to assess the effects on farm price and returns (and also on quantity) of a generic advertising program funded by a producer levy. We begin by considering separately the gross effects and benefits of the outwards shift in demand following a successful advertising program, and then the effects of the levy to fund the program. These two effects are then combined to assess the net effects on farmers of the program.

The current situation, or base case scenario, without the generic advertising program is shown in Figure 1. The industry supply curve or marginal cost curve, S=MC, is upward sloping, and demand at the farm level, D, is downward sloping. Together, the demand and supply curves determine an initial equilibrium at E, with a price (at the farm level) of P and quantity produced and consumed of Q. The quasi-rents to producers for their land, capital and managerial expertise, net of the opportunity cost of these resources if employed elsewhere in the economy, is known as “producer surplus”. This is the area above the supply curve and below the price line, namely area APE.

Figure 1: Market equilibrium with no generic advertising program

 

 

Figure 2: Market equilibrium with a generic advertising program

 

 

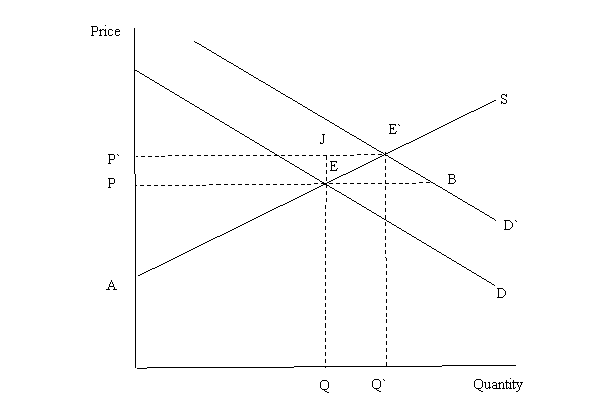
Effective generic advertising shifts the demand curve outwards from D to D`, as shown in Figure 2. At the initial price P, the expansion of demand due to advertising is the distance EB, which in later sections will be referred to as the derivative dQ/dA. A new market equilibrium is given at E`, with a higher price P` and a larger quantity Q`. The gross gain to farmers from advertising as measured by extra quasi-rents or increases in producer surplus is given by the area PP`E`E, comprising increased revenue on the initial sales of Q, area PP`EJ, and a relatively smaller area EJE`, which is the surplus on the additional output. So, a first approximation of the gross gain to producers from the demand expansion effect of advertising is the increase in farm price P`-P times the initial output Q.

Generally, the more effective the advertising program is in shifting demand, the larger will be the increase in the farm price, and the larger the benefits to farmers. Further, for any advertising-induced demand expansion, EB, the increase in farm price and farmer returns will be greater the less elastic (more steeply sloped) is either the demand curve or the supply curve. In the extreme cases where either the demand curve or the supply curve is perfectly elastic (horizontal), the farm price remains unchanged and farmers gain no benefits from advertising.

Figure 3: Market equilibrium with a per unit levy

 

 

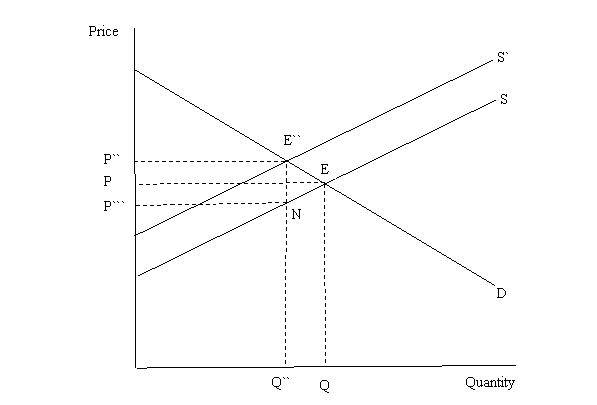
Figure 3 shows the effect of the levy to fund the advertising program on farm returns. The farm supply or marginal cost curve shifts upwards by the levy from S to S` because costs rise. The new equilibrium at E`` has a higher farm price P`` and a reduced quantity Q``. The farm price rises by less than the levy, so that the after-levy return received by farmers falls to P``` = P`` - L, where L is the levy per unit of production. Producer surplus is reduced by P```PEN.

Note that some of the levy cost which initially is paid by farmers is actually passed on to buyers as a higher price. The more inelastic is demand relative to supply, the higher the proportion of the levy that is passed forward to buyers. In the extreme case where demand is perfectly price inelastic (vertical), all of the levy is passed on to buyers and farmers gain so long as the advertising has a positive effect on sales.

The net effects of a generic advertising program funded by a levy can be determined visually by comparing the results from Figures 2 and 3. So long as the farm price increase effect of the advertising-induced increase in demand, PP` of Figure 2, exceeds the farm price reduction effect of the levy, P```P of Figure 3, there is a net increase in farm price, and farmer returns increase. Alternatively, so long as the area PP`E`E in Figure 2 exceeds the area P```PEN in Figure 3, farmer returns increase. In the following sections we derive explicit formulae to measure these net gains.

In Figure 2 and in the algebraic models that follow, the assumption is that advertising only affects the intercept of the retail demand curve (the “a” term in equation 1 below). Some commentators believe that advertising also may affect the slope or elasticity of the retail demand curve (the “b” term in equation 1 below) (Quilkey, 1986). For example, advertising to establish product differentiation for a particular product relative to other food products would work to reduce the elasticity of demand for the advertised product. If this effect is to swivel demand at the current price, a less elastic retail demand is beneficial for farmer returns if the supply curve shifts inwards, eg because of a drought, but it results in lower returns in the event of an outwards shift of supply, eg because of technical change. However, to date the empirical literature on estimates of the effects of generic advertising on the elasticity of demand is very limited, and there is little evidence of any significant effects. Thus, while it may not be the case in future studies, in this case we decided not to formally investigate the alternative interpretation.

3.2.2 Perfectly Competitive Model

In this section we make the simplifying assumption that processors and retailers of the farm product, as well as farmers, act as competitive price takers. The formal model presented here to quantify the effects of a generic advertising program funded by a levy on the farm price and on farmer returns follows a more comprehensive survey reported in Freebairn and Alston (2001). For simplicity the initial focus is on a non-traded model.

The formal theoretical model has a retail demand function, a marketing margin which is assumed to be a constant charge per unit of farm product for the costs of processing and retailing the product, a farm supply function, and a link between the retail price, the farm price, and the net return price to the farmer. For simplicity we assume a constant transformation ratio for the farm product through to the retail product, which allows us to use a common quantity in all equations. Also for simplicity we use price dependent retail demand and farm supply functions as follows

P_r = a – bQ                                                                                                           (1)

P_f = P_r – M = a – M – bQ                                                                                       (2)

P_p = c + dQ                                                                                                           (3)

P_f = P_p + L = c + L + dQ                                                                                        (4)

A = LQ                                                                                                                  (5)

where P denotes price, Q denotes quantity, M is the fixed processing and retailing cost per unit product, L is the levy, the subscripts denote r for retail, f for farm and p for net producer prices, and a, b, c and d are parameters. In (5), A represents the advertising budget which shifts out the retail demand curve via an increase in the parameter a, and LQ is the levy revenue. All available revenue is spent in any one period.  Figure 4 shows equations (1) through (4) as they determine the initial prices, P_r, P_f and P_p, and quantity, Q.

Figure 4: Market equilibrium with a generic advertising program and a levy

Equations (1) through (4) can be solved for the net producer price, P_p, as

P_p = (bc + da – dM – dL) / (b + d)                                                                      (6)

where all the terms are as defined above. Note that an increase in quantity demanded due to a successful advertising program increases the parameter a, and in turn the net producer price, while an increase in the levy reduces the net producer price[1].

Now, advertising, A, increases the quantity sold at retail and shifts the parameter a as

 (da / dA) dA = (dP_r / dA) dA = (dP_r / dQ) (dQ / dA) dA = -b (dQ /dA) dA             (7)

Then, using (7), and taking the derivative of (6), the gross effect of advertising which shifts quantity demanded, dQ / dA, on the net farmer price, P_p, is

 (dP_p / dA) dA = (- bd / (b + d)) (dQ / dA) dA                                                         (8)

Using (5), dA = Q dL + L dQ ≈ Q dL, (and this is an identity QL for a levy jump from zero), and substituting into (8), we have

 (dP_p / dA) dA = (- bd / (b + d)) (dQ / dA) Q dL                                                      (8`)

Taking the derivative of (6) with respect to the levy, L, the effect of the levy to fund the advertising is to reduce the net producer price by

 (dP_p / dL)  dL= (-d / (b + d)) dL                                                                            (9)

Comparing (7) and (8), a generic advertising program funded by a levy results in a net increase in farmer returns if (8`) ≥ (9). For a particular increase in the levy rate, from zero to L, so that dL = L, the required minimum or break-even advertising response dQ / dA can be derived from (8`) and (9) as

dQ / dA > (1 / b)  L = E Q (L / P_r), or                                                                   (10)

 (dQ / dA) / Q > E (L / P_r)                                                                                    (10`)

where, dQ / dA is the required increase in sales due to advertising, and (dQ / dA) / Q is the proportionate increase in sales due to advertising, E is the absolute value of the elasticity of demand (namely, (dQ / dP_r) (P_r / Q) ), and L / P_r is the levy as a proportion of the retail price.

Equating (8`) with (9), we derive the Dorfman-Steiner rule for the optimal advertising intensity, namely

A / P_rQ = L / P_r = N / E                                                                                        (11)

where, (A / P_rQ) is the advertising budget as a share of sales, L / P_r is the levy as a proportion of price or the ad valorem levy rate,  N is the elasticity of quantity demanded with respect to advertising (namely (dQ / dA) (A / Q) ), and E is the absolute value of the own-price elasticity of demand.

Equation (10) is the critical formulae for assessing whether a generic advertising program funded by a levy will increase the net farm price and thereby farmer returns. It has some very important implications, including:

• The more effective is the advertising in increasing demand, that is, the larger is dQ / dA, the larger should be the advertising budget and the larger the levy, L;
• The less price responsive or elastic is retail demand, that is, the larger is b or the smaller is E, the less is the required response of sales to advertising for the program to be worthwhile. In the extreme, if demand is non-responsive to price changes, only a very small advertising response is required. As demand becomes less and less price responsive, consumers bear a higher share of the levy and the demand shift results in a larger increase in the farm price; and
• No knowledge of the slope or elasticity of the farm marginal cost or supply function is required to assess whether an advertising program is worthwhile.

3.2.3 International Trade

Most Australian agricultural products are traded internationally (primarily as exports but a few as imports). It is straight forward to extend the non-traded model of the previous section to allow for international trade. In the case of an export product, the demand curve is disaggregated into a domestic demand component and an export demand component (or rest of world demand less rest of world supply). The generic advertising program can be directed at the domestic demand, at the export demand, or at both.  For an import-competing product, the supply curve is disaggregated into a domestic supply component and an import supply component (or rest of world supply less rest of world demand). Kinnucan (1999), Cranfield and Goddard (1999) and Kinnucan and Myrland (2000) have developed models where the advertised commodities are exported or imported.

Consider an export product. Initially and to simplify, consider the special case where the domestic and international products are homogeneous or perfect substitutes, and where there are no government policy interventions, so that there is one price. Later these assumptions are relaxed. Figure 5 illustrates.

Figure 5: Market equilibrium for an exported product

 

 

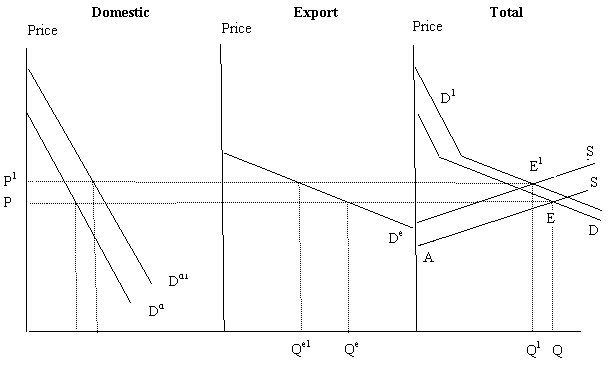
Before advertising, domestic demand is D^d, export demand is D^e, and total market demand is D = D^d + D^e. With initial supply S, market equilibrium at E is given by price P, quantities Q^d, Q^e, and Q = Q^d + Q^e, and producer surplus APE in the right hand side panel.

Now, suppose a levy L is collected on all Australian production to provide advertising funds A = QL for use in a generic advertising program to increase domestic sales. As a result, advertising shifts the domestic demand curve out to D^d1, export demand does not change, and total demand shifts out to D¹ = D^d1 + D^e. The levy shifts the supply curve upwards to S¹ = S + L. The new equilibrium is E¹. Farmers gain if the price increment effect of the advertising exceeds the price reduction effect of the levy so that the net farm price rises and production increases. Figure 5 as drawn has farmers losing,

with the new equilibrium price higher at P¹, domestic sales higher at Q^d1, but export sales much lower at Q^e1, and total sales and production lower at Q¹. Producer surplus decreases.

A formal model along the lines of that in section 3.2.2 can be expressed as follows

Q^d = a^d – b^dP                                                                                                   (12)

Q^e = a^e – b^eP                                                                                                   (13)

Q = Q^d + Q^e                                                                                                     (14)

Q = c + dP_f  = c + d (P – L)                                                                             (15)

A = QL                                                                                                            (16)

where, Q is quantity, with the superscripts d and e for domestic and export, P is price, with subscript f for farm net return, L is the levy, and A is advertising.

The net farm return can be derived by solving (12) through (15) for P_f  to give

P_f = [a^d +a^e – c –(b^d +b^e)L] / [b^d + b^e + d]                                                       (17)

Taking the derivative of (17), the effect of advertising to increase domestic sales on the farm net return is given by

 (dP_f / dA) dA = [1 / (b^d + b^e + d)] (dQ^d / dA) dA                                             (18)

and from (16) using dA ≈ Q dL,

 (dP_f / dA) dA  = [1 / (b^d + b^e + d)] (dQ^d / dA) Q dL                                         (19)

Taking the derivative of (17) with respect to the levy L, the effect of the levy on the net farm price is given by

 ( dP_f / dL) = -[ (b^d +b^e) / (b^d + b^e + d)] dL                                                       (20)

A generic advertising program for domestic sales funded by a levy results in a net increase in farmer returns only if (19) ≥ (20). For an increase in the levy from zero to L, the break-even advertising response dQ^d / dA required to increase farmer returns is

 (dQ^d / dA) / Q > [-(b^d + b^e) / Q] L = (w^d E^d + (1 – w^d) E^e ) L / P                      (21)

Imposing the equality on (21), and with some further manipulation, the profit maximising advertising intensity, A / PQ, can be expressed as

A / PQ = ( w^d N^d) / [ w^d E^d + (1 – w^d) E^e]                                                          (22)

where N^d is the elasticity of domestic sales with respect to the generic advertising, E^d is the absolute value of the domestic demand price elasticity, E^e is the absolute value of the export demand price elasticity, and w^d is the share of production for domestic sales.

From (22), the profit maximising advertising intensity and levy rate will be greater the larger is the response of domestic sales to advertising, the larger is the relative importance of domestic sales in total production, and the less price elastic is either or both of the domestic and export demand curves. When domestic sales dominate, that is when w^d approaches unity, (22) reduces to the non-traded model rule given in equation (11). If Australia is a “small trading country” unable to affect the world price, the export demand elasticity E^e approaches infinity, and the profit maximising advertising level and levy become zero. Here, domestic advertising affects only the mix of sales between the domestic and export markets, but not the world and domestic price. The same result holds for an import competing industry when Australia is a “small country” importer.

Important caveats to our small country story on the ineffectiveness of generic advertising in improving farmer returns are the assumptions of product homogeneity and of no trade or other policy interventions. If the domestic and rest of world products are regarded as imperfect substitutes, whether because of intrinsic physical differences or because of perceived differences, then the domestic price will differ from the world price (typically the domestic price is higher), and advertising of the domestic product can increase domestic sales of the relatively higher-priced domestic product. Developing breakeven rules for a heterogeneous product environment is another large area for future work,

Somewhat similarly, domestic two-price schemes, and the current domestic consumption levy arrangements on sugar and fluid milk, mean that generic advertising to increase domestic sales can increase producer returns. Strict phytosanitary regulations on imports, for example on shell eggs, salmon and some horticultural products, effectively mean that some Australian agricultural products are closer to a non-traded model than an international trade model.

3.2.4 Post-Farm Exercise of Market Power

The high levels of concentration in the post-farm stages of the marketing chain for many agricultural products raise questions about the effects of the exercise of market power on the returns to farmers from a generic advertising program. In many industries, because of economies of scale, the low value and bulk nature of agricultural products and other reasons, a few firms dominate the manufacture of agricultural products. Also, the two main supermarket chains account for up to 80 per cent of retail sales of some food product groups[2].

In order to assess the implications of market power on producer returns from generic advertising funded by a levy, this section initially explores the extreme cases of the post-farm sector acting as a monopolist exploiting market power in setting retail prices and then as a monopsonist exploiting market power in setting farm prices. The use of such market power clearly reduces the net price received by farmers, and alters the details of the effects of both an advertising-induced increase in retail demand and of the funding levy on the farm price. However, these models reach the same conditions as given in equation (10) for the competitive model, for a generic advertising program to increase net farm returns. The section then briefly refers to some other non-competitive behaviour models, including conjectural variations models and multi-stage post-farm non-competitive models, and it refers to numerical simulations which also find that market power at the post-farm stages has very little effect on the conditions required to improve returns to farmers.

Monopoly

Consider initially the case where the post-farm sector behaves as a monopolist. The market situation is as described in equations (1) through (5) above, with a retail demand function, a constant per unit post-farm cost of processing and retailing, a farm supply function with a per unit levy, and the advertising budget identity. From the retail demand equation (1), the monopolist’s marginal revenue function, MR, is given by

MR = a – M – 2bQ                                                                                            (23)

Then, equating MR of (23) with the price of the farm supply equation (4), the net producer price, P_p, can be derived as

P_p = (2cb + da – dM – dL) / (2b + d)                                                               (24)

where all terms are as defined above. Note that the net farmer return with monopoly in (24) is less than in the perfectly competitive model in (6), and the difference is greater the less price responsive is retail demand to P_r, or the larger is b. Figure 6 illustrates a comparison of the quantity and price outcomes for a monopoly relative to perfectly competitive market behaviour.

Figure 6: Market equilibrium for a monopoly

 

 

The effects of an advertising induced shift in demand, (dQ / dA) dA ≈ (dQ / dA) Q dL, on the net farm price P_p can be derived as

 (dP_p / dA) = ((-bd) / (2b + d)) (dQ / dA) Q dL                                                 (25)

and the effects of the levy L to fund the advertising program on the net farm price can be derived as

 (dP_p / dL) = (-d / (2b + d)) dL                                                                        (26)

where all terms are defined as above.

A generic advertising program funded by a levy on farm production increases the net farm price if (25) > (26), or if

dQ / dA > 1 / (bQ) = E (L / P_r )                                                                       (27)

A Dorfman-Steiner optimal advertising intensity ratio equivalent to (11) also can be derived.

We can compare the assessment for a competitive post-farm sector with the assessment for a monopolistic post-farm sector. In terms of the effects of the advertising-induced shift in demand on the net farm price, the gains for farmers are larger under competition than under monopoly, ie (8`) > (25). But also, less of the levy is borne by farmers under a monopoly than under competition, ie (9) > (26). Essentially these outcomes arise because the monopolist changes quantity by less than a competitive structure in response to changes in retail demand or farm costs. Combined, these effects offset each other, so that the decision rule for farmers on whether they gain from a generic advertising program funded by a farm production levy is the same for a competitive model, equation (10), or for a monopoly model, equation (27)[3].

Monopsony                                                                                     

If the post-farm sector recognises it has market power in its purchases of the farm product, and that the farm supply curve is upward sloping, it will choose an output level to equate its marginal factor cost, MFC, with the retail price less marketing costs. Figure 7 illustrates the comparison of a monopsony market outcome with a competitive model outcome. Monopsony reduces quantity and the net producer price.

Figure 7: Market equilibrium for a monopsony

 

Q d Q d1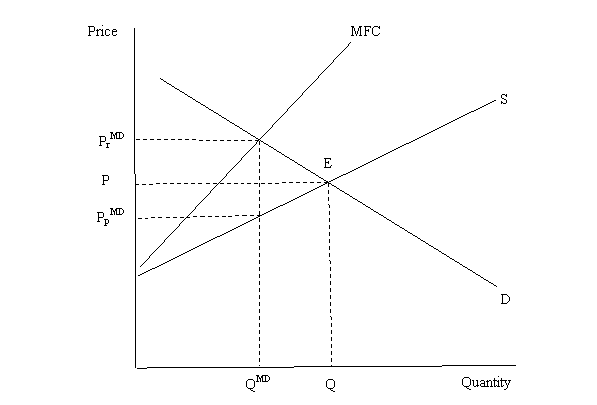

Formally, for the set of equations (1) through (5) describing the market, the MFC function is derived from the farm supply function (4) as

MFC = c + L + 2dQ                                                                                         (28)

Then, equating (2) with (28), the monopsony output Q can be derived, and substituting into (4), an equation for the net producer return can be derived as

P_p = ( ab + cd + da – dM – dL) / (b + 2d)                                                       (29)

Following the same procedures as for the perfect competition and monopoly models, expressions for the effects of an advertising-induced increase in retail demand, and for the effects of the levy on farm production to fund the advertising, on the net farm return can be derived as

 (dP_p / dA) dA = ((-bd) / (b + 2d)) (dQ / dA) Q dL                                            (30)

 (dP_p / dL) dL =  ((-d) / (b + 2d)) dL                                                                (31)

The program would increase net farmer returns if (30) > (31), or if

dQ / dA > (1 / bQ) = E (L / P_r )                                                                        (32)

Compared with the outcomes from the perfect competition model, monopsony behaviour results in smaller net producer price changes when we consider the effects of the demand expansion effect of advertising, or the levy imposition effect, separately. However, when the two effects are combined as part of a levy-funded generic advertising program, again they offset each other. Thus, the three quite different models of market behaviour result in the same decision rule on whether the program will or will not increase farmer returns.

Combined Monopoly and Monopsony

It is straightforward to extend the model so that the post-farm sector fully exploits market power against both consumers and farmers. The post-farm firm would choose a quantity which equates the marginal revenue of (23) with the marginal factor cost of (28). Quantity would be smaller again than with either monopoly or monopsony alone, and the required net farm return to induce production of the smaller quantity also would be less. For our purposes, the most relevant result is that the competitive model rule for deciding on whether a generic advertising program funded by a farm levy given in equation (10) also applies if the post-farm sector behaves as a monopoly and monopsony.

Conjectural Variations Model

The monopoly and monopsony models described above assume there is just one firm responsible for the processing and retailing of agricultural products. Clearly this model over-simplifies reality. A more realistic model would have several post-farm marketing firms. This situation is referred to as oligopoly when using market power over consumers and as oligopsony when using market power over farmers. The literature contains a very large number of potential oligopoly and oligopsony models, and there are different models for different circumstances. The evolving state of the Australian industry cautions on pinpointing a particular model for a particular point in time.

Agricultural economists have made extensive use of the conjectural variations model to analyse the effects of advertising farm commodities. Examples include Holloway (1991), Alston, Sexton and Zhang (1997), Kinnucan (2003), Muth and Wohlgenant (1999), Sexton (2000), Zhang and Sexton (2002) and Wohlgenant and Piggott (2003).

Conjectural variations models embrace as special cases the competitive, monopoly, monopsony and monopoly-monopsony models already discussed. In essence, on the oligopoly side, the post-farm sector is assumed to equate a weighted average of the retail demand function and marginal return function with marginal cost in setting a retail price, and on the oligopsony side it is assumed to equate a weighted average of the farm supply function and the marginal factor cost function with marginal revenue in dealing with farmers. Formally, output is chosen to equate

s P_r + (1 – s) MR = w P_f + (1 –w) MFC                                                            (33)

where P_r, MR, P_f and MFC are as defined above, and s and w are weights. These weights, or conjectures, are estimated as one set of parameters. Typically the estimated conjectures imply only small deviations from the special case competitive model outcomes, that is, estimates of s and w are close to unity.

Numerical simulations of the returns to farmers from generic advertising programs using conjectural variations models to represent the use by the post-farm sector of oligopoly and oligopsony behaviour, especially those by Kinnucan (2003) and Wohlgenant and Piggott (2003), find that the estimated returns are not sensitive to different assumptions about the exercise of market power.

Multi-stage Post Farm Sector

The models discussed so far have grouped all the post-farm marketing activities of transport, storage, processing, wholesaling and retailing into a single sector, or alternatively, these post-farm activities have been treated as being undertaken by a single vertically integrated firm. Another option, which brings additional complexity, is to explicitly recognise the different stages of farmers, processors and retailers.

Several papers have developed models for multi-stage production systems with players at two stages exercising market power in non-cooperative games, but they treat the farm level supply as a constant

cost, and in effect assume a perfectly elastic supply. Examples include Cotterill et al. (2000), Cotterill (2000), Dhar and Cotterill (2002), Eales and Brinkley (2003), Kadiyali et al. (1996) and Putsis and Dhar (1998). A vast number of different game theory models of oligopoly behaviour are available in the literature, and each has different implications for outcomes of prices, quantities and advertising.

One important result (and apparently a quite robust result) of the independent exercise of market power by non-cooperating firms in a multi-stage production system game is that output is less than if they had co-operated or acted as an integrated firm. Take for example the so-called “double marginalisation” result for two monopolists (Figure 8) discussed in the utility regulation literature by King and Maddock (1996), or vertical Nash behaviour for marketing.

Figure 8: Market equilibrium for double marginalisation

 

Retail demand is given by D_r and a constant farm marginal cost (equal to average cost) is given by MC. Suppose there are two stages from farm to retail, manufacturing and retailing, and each stage has constant, equal to zero, production costs. An integrated manufacturer and retailer would choose quantity Q_m to maximise profit.

Now, assume two separate firms for each production step. The retailer sees its marginal revenue curve as MR_r. A fully informed manufacturer, knowing that the retailer would use its monopoly position, would see the demand curve for the manufactured product as D`=MR<sub>r</sub>, and from this its marginal revenue curve is MR`. Then, the manufacturer would choose quantity Q_dm to maximise its profits. Double marginalisation has further reduced industry quantity, including that purchased from farmers.

It seems reasonable to hypothesise that if the model described in Figure 8 was extended to have a rising farm supply or marginal cost curve, the effect of having more than one production step with firms exercising market power in a non-cooperative way would, compared with the one-step production model, result in a smaller quantity and lower farm price. In addition, a rising farm marginal cost curve invites the post-farm firms to indulge in oligopsony pricing of the farm product to increase their profits.

From the perspective of decisions on generic advertising programs funded by a levy on farmers, it seems reasonable to extrapolate the findings of the single post-farm models that the decision rule of (10) derived for a competitive model also will provide a satisfactory guide.

3.2.5 Advertising Reactions

So far we have considered a generic advertising program in an environment where the program is assumed to cause no changes or reactions in brand advertising programs by processors and retailers. In principle, firms in the post-farm sector could increase or reduce their own advertising programs as a strategic reaction to the farm-funded generic advertising program. This section considers some of the potential implications of such reactions for the returns to farmers from their advertising program.

Consider a simple model in which the farm product is sold as two brands at the retail level. These brands could be a processor or retailer propriety brand and a generic brand, or two propriety brands, and the two brands are partially differentiated and regarded as imperfect substitutes by consumers. Demand for each brand is a function of the prices for the two products, propriety brand advertising, and a farmer-funded generic advertising program. Formally,

Q₁ = f( P₁, P₂, A₁, A₂, A)                                                                                   (34)

Q₂ = f( P₁, P₂, A₁, A₂, A)                                                                                   (35)

Q = Q₁ + Q₂                                                                                                    (36)

where Q₁ and Q₂ are quantities of the two retail brands, Q is total quantity, P₁ and P₂ are the prices of the two brands, A₁ and A₂ are propriety brand advertising, and A is generic advertising. Other things constant, we could expect A_i, for i = 1, 2, to increase sales of Q_i and reduce those of Q_j, and for generic advertising A to increase sales of both Q₁ and Q₂.

Our analysis so far has assumed a change in generic advertising, A, causes no reactions in the advertising levels for the brands A₁ and A₂. Formally, in the context of our simple model we assumed

dQ / dA = dQ₁ / dA + dQ₂ / dA                                                                        (37)

A more general model would allow for the propriety advertising expenditures to respond to the generic advertising. Then, the net response of farm sales to generic advertising would involve extra terms, namely, 

dQ / dA = dQ₁ / dA + dQ₂ / dA  + (dQ₁ / dA₁ +dQ₂ / dA₁) (dA₁ / dA)

+ (dQ₁ / dA₂ + dQ₂ / dA₂) (dA₂ / dA)                                                               (38)

If the net effect of propriety brand advertising, A₁ and A₂, is to increase aggregate sales, that is if an increase in A_i increases the sales of Q_i more than it reduces the sales of Q_j, which is a reasonable assumption, then the reactions of the propriety brand advertisers to an increase in generic advertising in (38), dA_i / dA, determines whether the generic advertising effects are augmented by, or diminished by, these reactions. If the propriety advertising budgets are reduced, the generic advertising crowds out other advertising, and (38) < (37). But, if the generic advertising stimulates an increase in propriety brand advertising, perhaps as a form of a prisoners’ dilemma game or a retaliatory reaction, then (38) > (37) and the first round benefits of the generic advertising program are augmented. The direction of effect of propriety brand advertising to generic advertising is an empirical question, as also is the magnitude of that response.

To our knowledge, no published study of the advertising of agricultural products has considered estimating the strategic reactions of brand advertising to changes in the level of generic advertising, that is estimating the terms dA_i / dA in (38). Clearly such a study would place enormous requirements on available data[4].

3.2.6 Factor Substitution

So far we have made the simplifying assumption that a unit of farm product is transformed into a fixed number of units of retail product. Technically, the assumption is that the elasticity of substitution of the farm product for the non-farm inputs used in producing retail products is equal to zero. Importantly for our analysis of the effects of a farm levy-funded generic advertising program, the constant rate of transformation assumption means that a shift of the retail demand curve due to advertising has the exact same effects on prices and quantities as a shift of the farm supply curve due to the levy.

If production technology allows the post-farm sector to change the transformation ratio of the farm input to the retail product, the elasticity of substitution between the farm and post-farm inputs exceeds zero. With such technology, if there are changes in the relative cost of the farm product to the cost of labour, equipment and materials used in processing and retailing agricultural products, the post-farm sector will be able to substitute the relatively cheaper input for the more expensive input. Then, changes in demand due to advertising will have different effects on the pattern of farm and retail prices than will changes in the levy affecting farm supply[5]. Importantly, as shown clearly analytically and with illustrative numerical examples by Wohlgenant (1993), Kinnucan (2003) and Wohlgenant and Piggott (2003), the benefits to farmers of generic advertising programs are significantly reduced as the elasticity of substitution increases from zero as in our simple model.

Further, Wohlgenant and Piggott (2003) show that the degree of input substitution is more important than market power in influencing producer returns, and thus should be the focus of more analytical work. However, in Australia at least, much of the available data are too aggregated and/or are calculated from fixed-proportions assumptions which does not allow ready estimation of these input substitution parameters.

3.3 Generic Advertising Funded by a Lump Sum

While in most cases the generic advertising budget will be funded by a levy, in some special cases it may be more appropriate to use a model which assumes the funds are in the form of a lump sum. Examples include funds held over from previous years, a levy or charge per production unit rather than per unit of production, and direct grants to the industry from government. The important comparison of a lump sum funding model versus a levy funding model is that the levy as a variable cost shifts the farm supply curve upwards, whereas the lump sum as a fixed cost has no effect on the farm supply curve. Importantly, the lump sum funding cost is borne entirely by farmers, whereas some of the levy funding cost is passed on to buyers as higher prices than would otherwise occur.

There are at least two important sets of differences in the implied decisions on generic advertising programs for farmers without supply control when comparing levy funding versus lump sum funding of the program. First, a larger advertising program will be optimal with levy funding, or to put it another way, the required advertising-induced quantity increase for farmers to gain will be less, than is the case under lump sum funding. The intuitive reason is that the levy cost is in part passed onto buyers, whereas the lump sum is borne entirely by farmers. Formally, for the simple competitive model, the profit maximising advertising intensity, A / PQ, for the levy funding model is the Dorfman-Steiner rule derived as (11),

A / PQ = N / E                                                                                               (11)

where, N is the advertising response elasticity, and E is the absolute value of the own-price demand elasticity. But, for the lump sum funding model, the profit maximising advertising intensity is the Nerlove-Waugh rule

A / PQ = N / (E + S)                                                                                      (39)

where, N is the advertising response elasticity, E is the absolute value of the own-price demand elasticity, and S is the own-price supply elasticity (for a summary see, for example, Freebairn and Alston, 2001). For a positive supply elasticity, (11) > (39), and the more elastic is supply the greater the optimal generic advertising budget for levy funding relative to lump sum funding (see also Mounter et al. 2004).

Second, our finding that the exercise of market power in the post-farm sector, whether in the form of monopolistic or monopsonistic behaviour, had little effect on the profit maximising advertising intensity with levy funding, is no longer the case with lump sum funding. Relative to a competitive model, the exercise of market power by the post-farm sector significantly reduces the farm price increase flowing from an advertising-induced increase in retail product demand. This is the identical case for both levy-funded and lump sum-funded programs, But, with levy funding, the smaller quantity response by the post-farm sector exercising market power results in most of the levy being passed forward to buyers as higher prices, while the lump sum funded program leaves all of the costs with the farmer. Thus, market power is much more important in a lump sum funding world than in a levy funding world.

3.4 Brand Advertising and Supply Control

Most of the marketing and industrial organisation literature on advertising refers to advertising decisions on brand products where the firm has both some market power and control over quantity supplied. Advertising expenses are treated as a lump sum cost rather than as a variable cost in these models. Since generic advertising programs in some cases will be in markets where brand advertising already is in place, it is useful to briefly cover brand advertising.

Consider a firm with a single brand for a differentiated product so that its demand or average revenue curve is downward sloping. For simplicity ignore any strategic interactions with other brands and firms, as best fits a monopoly or monopolistic competitive industry rather than an oligopoly. Then, as shown earlier in Figure 6, the firm chooses output Q=Q^m to maximise profit at the level where marginal revenue, MR, equals marginal cost, MC=P^m_f, and price P=P^m_r is taken off the demand curve.

Advertising to increase sales, dQ / dA, shifts out the demand curve. For a small increase in sales the firm gains P – MC per unit of extra sales, so that the marginal return from advertising is (dQ / dA) (P – MC). This is then compared with the marginal cost of advertising, which as a lump sum charge falls entirely on the firm, and can be normalised to unity. Equating marginal benefits and costs of advertising, the profit maximising advertising level is given by

 (dQ / dA) (P – MC) = 1                                                                                    (40)

Using the fact that (P – MC) / P = E, and some minor manipulation, the profit maximising advertising intensity, A / PQ, is given by the Dorfman – Steiner result

A / PQ = N / E                                                                                                  (41)

where as before, N is the advertising elasticity of demand, ( dQ / dA) (A / Q), and E is the absolute value of the own-price elasticity of demand, ( dQ / dP) (P / Q). The greater the advertising response, and the less elastic is demand, the greater would be the profit maximising brand advertising intensity.

The model in Figure 6, and formula (40) and (41), also show that advertising aimed at establishing brand product differentiation and reducing the elasticity of demand increases the price mark-up, P – MC, which in turn increases profit per unit of output.

Brand advertising can be used as one of several techniques to raise barriers to market entry to new brands and producers as a longer term strategy to protect and enhance profits. The fixed cost characteristic of brand advertising adds to the magnitude of scale economies, and advertising backed-up by quality maintenance helps lock-in buyers to established brands over new brands.

3.5 The Advertising Response Function

In its general form we can think of the retail demand function as

Q = f( P, A, Z)                                                                                                 (42)

where, Q is quantity demanded, P is price, A is advertising, and Z is a set of other explanatory variables such as income. In this section we comment on the relationship between advertising expenditures and the time profile of increases in sales of Q, and on the algebraic form of this relationship as it bears on the derived marginal productivity and elasticity estimates.

So far we have made the simplifying assumption of an instantaneous response of sales to advertising with no carry-over effects on future sales. That is, in the formula all the advertising effects are represented by dQ / dA.  Should advertising today affect sales in the future as well as today, that is there are carry-over advertising effects, an appropriate specification of (42) would have lagged as well as current levels of advertising as explanatory variables, and the derivative dQ / dA would include the lagged as well as the current period effects. In principle, the modelling of the preceding sections readily generalises to include lagged responses of sales to advertising.

From a practical perspective, whether advertising has effects on future period sales as well as current period sales depends on the observation period imposed, the product and the particular advertising program, and ultimately the appropriate answer is an empirical one. In those analyses where the imposed period of analysis is a year, the lagged effects of sales on advertising are likely to be small relative to the current year effects. If a shorter observation period of, say, a quarter, is being used, the case for testing for lagged responses becomes more compelling.

The algebraic form of the demand relationship (42) predetermines key properties of the marginal advertising response, dQ / dA, and the advertising elasticity, N = (dQ / dA) (A / Q). A simple linear relationship imposes a constant marginal productivity result which implies that if some advertising is worthwhile, an infinite advertising budget is worthwhile. Ultimately, the marginal productivity of advertising must decline. Declining marginal productivity of advertising can be achieved by, for example, adding a quadratic term A², or by entering the advertising variable in the form (1 / A). Alternatively, expressing the demand function (42) as linear in logarithms gives a constant advertising elasticity and a declining marginal productivity of advertising. With some consideration of the acceptable theoretical implications, the final choice of a functional form should be guided also by the form which best fits the data.

3.6 Some Conclusions Relating to the Literature

We have considered the returns from advertising in three different contexts. A model with levy funding of a generic advertising program and farmers choosing output to equate the net farm return with marginal cost is the most appropriate model in most cases. In a few cases a model with lump sum funding of the generic advertising program and no supply control may be more appropriate. Brand advertising by firms using lump sum funding and with firm direct control over supply is also found in some parts of the agricultural sector.

For the levy funding model, the effects of several different sets of modelling assumptions on the returns to farmers of advertising programs were explored. The simple closed-economy competitive model is readily generalised to allow for international trade, either exports or imports. The exercise of monopoly and monopsony market power by the post-farm processing and marketing firms do not greatly alter the net returns to farmers of a generic advertising program; but this is not the case with a lump sum funding arrangement. The greater the elasticity of substitution between the farm input and the off-farm inputs in producing retail products, with the simple model assuming a zero elasticity, the smaller the benefits to farmers of generic advertising funded by a levy. A generic advertising program may induce existing brand advertising programs to be increased or reduced, and such reactions will augment or reduce the gains to farmers, respectively.

Two key sets of formula for evaluating the benefits to farmers of a levy funded generic advertising program were developed. These two sets of formula refer to a break-even advertising quantum if farmers are to gain, and a rule specifying the farmer profit-maximising advertising intensity. To illustrate, the formulae for an exported product are repeated here, and a non-traded product is a special case. The break-even advertising quantum is

 (dQ^d /dA) / Q > (w^dE^d + (1 – w^d)E^e) (L / P)

where dQ^d / dA is the required increase in domestic market sales from the advertising program, Q is production or total sales, w^d is the share of production sold domestically and (1 – w^d) is the export share, E^d is the absolute value of the domestic market price elasticity of demand, E^e is the absolute value of the export market elasticity of demand, L is the levy per unit production, and P is the retail price. For a non-traded product, w^d = 1.

The advertising intensity which maximises farmer profits is

A / PQ = (w^d N^d) / (w^dE^d + (1 – w^d) E^e)     

where A / PQ is the advertising budget as a share of total receipts,  N^d is the elasticity of domestic sales with respect to the generic advertising program, and all other terms are as before. These formulae assume a constant rate of transformation of the farm product to the retail product (that is, an elasticity of substitution of zero), and that there is no change in any existing brand and other advertising programs.

4. Some Break-even Principles

This section combines the conceptual model formulae on the returns to farmers from generic advertising of domestic sales funded by a levy on production, and knowledge of the properties of the markets for a large number of Australian agricultural products, to estimate the minimum advertising-induced increase in sales necessary for farmers to gain.

The general formula developed for the minimum or break-even response from advertising if farmers are to gain is as follows

 (dQ^d / dA) / Q^d = [w^d E^d + (1 – w^d) E^e] (L / P) (1 – w^d)

where ( dQ^d / dA) / Q^d is the increase in domestic sales Q^d due to advertising A as a share of domestic sales, w^d is the share of output sold domestically and (1 – w^d) is the export share, E^d is the (absolute value of the) domestic own-price elasticity of demand and E^e is the (absolute value of the) export own-price elasticity of demand, and ( L / P) is the levy as a share of the domestic retail price.

This break-even formula refers to a competitive industry at both the farm and post-farm levels. It remains valid even when there is a wide range of forms of market power in the post-farm sector, although the exercise of market power may mean a different value for the domestic demand elasticity. The formula also assumes no changes up or down in advertising levels of existing brand advertising programs, which is a default assumption for which there is no empirical evidence to the contrary. Importantly, the formula assumes a constant rate of transformation of the farm product into retail product. For many cases this assumption of zero substitutability between the farm input and other inputs in producing retail food products is too strong; allowing for substitutability means the formula will underestimate the break-even advertising response. 

This general formula provides useful guidelines on the potential returns to farmers from generic advertising of products with different trade, own-price elasticity of demand, and levy rate characteristics. The greater the levy rate, the greater the required advertising-induced increase in sales. The more important are export sales as a share of production, the greater is the required advertising response. In particular, when Australia is a small country exporter, or importer, and the world price sets the domestic price, generic advertising will not increase farmer returns. Australian and international trade and agricultural policies clearly can, and do, alter the relationship between Australian and world prices. The larger the domestic demand and the export demand own-price elasticities, the larger is the required increase in domestic sales from generic advertising if farmers are to gain. We can use these guidelines to consider the different required advertising responses for different products that would be necessary for farmers to gain from a levy-funded generic advertising program.

Table 1: Some characteristics of the markets for Australian agricultural products

Product	Importance of Export Markets		Trade and Quarantine Restrictions
	Exports as share of production (%)	Australian exports as share of world exports (%)
Wheat	72	14	Single desk exporter
Barley	65	}
Oats	12	} <5 for feed grains
Sorghum	21	}
Rice	66	3	Single desk exporter
Canola	75	small
Cotton	95	10
Sugar	73	9
Dried vine grapes	27	small
Wine	50	small
Beef and veal	65	22	Some restrictions in export markets
Mutton	74	50
Lamb	35	25	Some restrictions in export markets
Pig meat	18	Small - competition from frozen product imports, specified countries	Quarantine against imports from most countries
Poultry	4	small	Quarantine against imports
Wool	100	68
Butter	64	17
Cheese	56	21
Milk powder	80	20
Eggs – shell	0	0	Quarantine against imports
Eggs – processed	Small	small
Apples	8	small	Quarantine against imports
Pears	17	Small
Peaches	38	Small
Apricots	16	small
Citrus	23	Small - some competition from juice imports
Bananas	0	0	Quarantine against imports
Potatoes	Small	Small - some competition from frozen product imports
Other vegetables	Small	Small - some competition from frozen product imports

Sources: wherever possible, values are 5 year averages over the period 1999/00-2003/04, drawn from data contained in Australian Commodities (recent issues) and IBIS Agricultural Industry Reports (recent issues).

Table 1 provides information about export shares of total sales, about Australian exports as shares of world exports, and about Australian trade and quarantine restrictions, for a wide range of products.

For many products, exports represent two-thirds or more of sales. These products include wheat, barley, rice, canola, cotton, sugar, beef, mutton, butter, milk powder and wool. For another group of products, export sales account for between one and two-thirds of sales, including wine, lamb, cheese and peaches. For all of these products, except wool and mutton, Australian exports represent less than 30 per cent of world exports. So even if the world export market is insulated from most of the Rest of the World trade by trade restrictions and agricultural policies, the scope for Australian exporters to exercise market power in the world export market is limited, and the own-price elasticity of export demand is likely to be high.

In the ORANI model of the 1980s, the authors considered export markets for Australian products to be characterised by fairly homogeneous products from the different exporting countries, with numbers of around -10 for the Australian own-price export demand elasticity. The updated and revised MONASH model of the 1990s and 2000s recognises product heterogeneity by country of export source, and uses much lower export demand elasticities of around -4 for traditional agricultural exports, and of -1.3 for wool (Dixon and Rimmer, 2002).

Another set of Australian agricultural products listed in Table 1 have relatively small exports, and/or the domestic market is protected from most import competition to a greater or lesser extent by quarantine restrictions. These products include oats, sorghum, dried vine fruits, pig meat, shell eggs, poultry, and most fruits and vegetables, although imported frozen and processed vegetables place a ceiling on the use of market power by the vegetable industries. For these industries, a non-traded model likely provides a satisfactory approximation for assessing the effects of a generic advertising program.

To apply the general break-even formula, we also need estimates of the domestic demand own-price elasticity and of the levy rate. For the levy rate L / P, we use three scenarios of 0.25 per cent, 0.5 per cent and 1 per cent. The latter is toward the maximum of observed programs (and for comparison, the levy rate for R&D purposes is around the 0.5 per cent level for most products). A range of own-price demand elasticities for the domestic market of 0.2, 0.5 and 1.0 are considered. In practice, for very few products is domestic demand estimated to be elastic.

Table 2: Estimates of the breakeven increase in domestic sales from generic advertising for different market conditions (minimum % increase in domestic sales for farmers to gain)

Market parameter setting			Levy as % of retail price
Domestic share of sales (Wd)	Absolute value of the own-price elasticity		0.25	0.5	1.0
	Domestic (Ed)	Export (Ee)
1.0	0.2	-	0.05	0.1	0.2
	0.5	-	0.125	0.25	0.5
	1.0	-	0.25	0.5	1.0
0.5	0.2	4	1.05	2.1	4.2
	0.5	4	1.125	2.25	4.5
	1.0	4	1.25	2.5	5.0
	0.2	10	2.55	5.1	10.2
	0.5	10	2.63	5.25	10.5
	1.0	10	2.75	5.5	11.0
0.2	0.2	4	4.05	8.1	16.2
	0.5	4	4.13	8.25	16.5
	1.0	4	4.25	8.5	17.0
	0.2	10	10.05	20.1	40.2
	0.5	10	10.13	20.25	40.5
	1.0	10	10.25	20.5	41.0

 

Table 2 reports estimates of the required percentage increase in domestic sales if a generic advertising program is to increase farmer returns. For example, if domestic sales are 50 per cent of total sales, the domestic demand elasticity is 0.5 and the export demand elasticity is 4 (both in terms of absolute values), a 0.25 per cent levy would need to increase sales by 1.125 per cent for farmers to gain. The table clearly illustrates that the required increase in sales rises with the levy rate, with the share of sales exported, and with both the elasticities of domestic and export demand.

The first part of Table 2, with w^d equal to unity, is for “non-traded” products, such as shell eggs, bananas and most vegetables. For a levy rate equal to 0.5 per cent of the retail price, advertising would need to increase domestic sales by 0.1 per cent for a demand elasticity of 0.2 and by 0.5 per cent for an elasticity of 1.0 for farmers to benefit from the program.

Required minimum percentage increases of domestic sales for products where the domestic and export markets each account for about a half of sales are shown in the middle part of Table 2. Wine, beef and veal, cheese, some of the grains and peaches are in this category. For a levy rate equal to 0.5 per cent of the retail price, advertising would need to increase domestic sales by at least 2 per cent if the export demand elasticity is around 4, and by at least 5 per cent if the export elasticity was around 10. The domestic price elasticity has little effect on the break-even advertising response.

It should be noted that these break-even advertising responses are greater than almost all credible advertising responses obtained from econometric studies. While this is not the place to present a detailed review of past attempts to estimate advertising response elasticities, it is instructive to examine some previous estimates for a well-studied subgroup of products – the fresh meat subgroup. Some previous results are reported in Table 3. Note the generally small response coefficients and the large proportion of negative responses, especially in the more recent studies that use more theoretically correct model specifications and estimation techniques.

The bottom part of Table 2 reports estimates of the required percentage increase in domestic sales for products from advertising where about 80 per cent of the sales are export sales. These products include wool, wheat, sugar and cotton. The break-even advertising response rate is yet higher, and further beyond available credible estimates. In effect, domestic generic advertising largely shifts a few sales from the export to the domestic market, with only a minimal, if any, increase in the world and domestic price.

Thus, under the assumptions used in this analysis, it is only for those products that are either non-traded or where trade accounts for a minority of output, that generic advertising of domestic sales funded by a levy on production is likely to generate positive returns to farmers.

Table 3: A selection of empirical studies on the returns to meat advertising

Study	Commodity	Country	Functional Form	Advertising Specification	Results
Funk, Meilke & Huff (1977)	Beef	Canada	Linear	Own & cross-advertising effects	Beef: 0.12 to 0.50 Pork: -0.04 to 0.13
Ball & Dewbre (1989)	Beef, Lamb & Pork	Australia	Linear	Current period, own, and cross-advertising	Beef: 0.25E-02,  -0.22E-02 Pork: 0 .13E-01,  0.42E-03 Beef: 0.037    Lamb: 0.009 Pork: 0.029 7:1 benefit-cost
Goddard & Griffith (1991)	Beef, Lamb & Chicken; Beef, Lamb & Pork	Canada Australia	Translog, AIDS & Log-log	Current period advertising for each meat type	Canada pork: -0.27 to 0.053 Australian pork:   -0.006 to 0.003
Hoover, Hayenga & Johnson (1992)	Beef	US	Linear & Multi-stage	Current period with 8 quarter carryover	Consumption rose 3% in response to TV advertising campaign
Jensen & Schroeter (1992)	Beef	US	Tobit model	Single period generic advertising	Persuasive advertising reduces demand
Ward & Lambert (1994)	Beef, Pork & Chicken	US	Rotterdam	Current & 1-year lag generic and brand advertising	Advertising elasticities: -0.005 to 0.03
Duffy (1995)	Pork Products	Canada	AIDS	1-year lag generic & brand advertising	Pork: 0.0006 to 0.101 Product: -0.0042 to 0.084
Piggott et al. (1996)	Beef, Lamb, Pork & Chicken	Australia	Single equation double log & share; LA-AIDS & AIDS	Own & cross- advertising effects, lagged up to 4 quarters	Beef: AMLC: significant APC: insignificant Lamb: AMLC: insignificant APC: insignificant Pork: AMLC: significant APC: insignificant
Cranfield (1996)	Beef	US Canada	Linear	Current, own & cross-advertising, generic & brand advertising	(w.r.t. beef demand) Canada beef: 0.003 Canada pork: -0.02 US beef: 0.090 US pork: -0.227

 

5. Implications

When farmers in a competitive production sector collectively levy each other to fund an advertising program directed at domestic consumers to increase sales of the retail product, and the levy is on a per unit basis, it represents an additional variable cost of production. Farmers gain from such a generic advertising program only if the advertising-induced rise in the farm price outweighs the levy-induced fall in the farm price, so that the net farm price rises.

For farmers to gain, the required increase in domestic sales due to the program has to be larger:

• The larger the levy rate as a share of the retail price;
• The smaller is the share of domestic sales in total sales; and
• The larger is the own-price domestic demand elasticity or the own-price export demand elasticity.

Thus farmers gain most when the advertising program is extremely effective in shifting domestic demand and requires only a small investment of levy funds, export sales are a small share of output, and domestic demand is very inelastic. For example, for a non-traded product, perhaps because of quarantine restrictions or because of very high transport costs, with a very low price elasticity, farmers can pass on almost all of the levy to consumers as higher prices and only a trivial response of sales to advertising is required to increase farmer returns. As well, the more effective is advertising, and the less-price elastic is demand, the larger should be the advertising intensity needed to maximise farmer returns.

Conversely, when Australia is a small country exporter (or importer), in the sense that our exports are so small a share of world trade that changes in Australian exports have no effect on the world price, and therefore on the Australian price, the export demand elasticity approaches infinity. In this situation, advertising of Australian sales has no effect on the price to farmers, and generic advertising can not improve farmer returns.

The implication here is that the characteristics of the markets for individual products are very important in determining whether a generic advertising program has any possibility of generating positive returns to farmers. For example, for non-traded products, such as shell eggs and bananas, for a levy rate of 0.5 per cent of the retail price, advertising would need to increase sales by 0.1 per cent for a demand elasticity of 0.2 and by 0.5 per cent for a demand elasticity of 1.0.

For products where about a half of the production is exported, for example beef, rice and dairy products, and assuming an export demand elasticity of 4 and a levy rate of 0.5 per cent of the retail price, generic advertising would need to increase domestic sales by about 2 per cent for a domestic demand elasticity of 0.2 and 2.5 per cent for an elasticity of 1.0. The required increase would be over 5 per cent for an export demand elasticity of 10. These break-even advertising responses are greater than almost all credible advertising responses obtained from econometric studies.

For products where exports account for about 80 per cent of sales, for example sugar, wheat and cotton, and assuming an export demand elasticity of 4 and a 0.5 per cent levy, generic advertising would need to increase domestic sales by around 8 per cent. Such increases are clearly well outside the range of possibilities.

The basic model evaluated in this study makes three crucial assumptions (no market power, no changes in brand advertising, no input substitution) that may have a bearing on whether a generic advertising program would be of benefit to farmers. First, the exercise of market power by firms in the post-farm sector will reduce quantity, increase the retail price, reduce the farm price and reduce farmer returns, but seems likely to have little effect on the net benefits to farmers of a levy-funded generic advertising program. Compared with a competitive model, the exercise of market power does dampen the benefits to farmers from the demand shift due to the advertising, but at the same time, the costs to farmers of the funding levy are similarly dampened by firms exercising market power. For this particular decision problem, market power would not seem to be much of a concern.

Second, if existing brand advertising programs are decreased as a result of a generic advertising program, the required minimum generic advertising response for farmers to gain would be increased.

Third, if there is some input substitutability (and there is growing empirical support for this fact), the basic model overestimates the gains to farmers from an advertising-induced increase in retail demand.

Interactions between brand and generic advertising and the issue of input substitution would therefore seem to have major implications for whether a generic advertising program funded by a per unit levy would be of benefit to farmers.

6. Further Research

Producer groups and their industry institutions contemplating generic advertising campaigns must be aware of the economic characteristics of the markets for their individual products, as these characteristics are crucial in determining whether a generic advertising program has any possibility of generating positive returns to farmers. The information provided in Tables 1 and 2 goes some way to describing the required information in very general terms, but more precise information would be required for such decisions for many individual industries. And of the required information, that relating to the price elasticity of demand in the domestic and export markets is the least reliable.

The basic model assumes no input substitution between the farm product and other inputs such as labour, equipment and materials used in processing and retailing agricultural products, in producing the product sold at retail. However, if the production technology allows the post-farm sector to change the transformation ratio of the farm input to the retail product, and if there are changes in the relative cost of the farm product to the cost of labour, equipment and materials, the post-farm sector will be able to substitute the relatively cheaper input for the more expensive input. Then, changes in demand due to advertising will have different effects on the pattern of farm and retail prices than will changes in the levy affecting farm supply, and the benefits to farmers of generic advertising programs are significantly reduced as the elasticity of substitution increases above zero. Further, Wohlgenant and Piggott (2003) show that the degree of input substitution is more important than market power in influencing producer returns, and thus should be the focus of more analytical work. However, in Australia at least, much of the available data are too aggregated and/or are calculated from fixed-proportions assumptions that do not allow ready estimation of these input substitution parameters.

Finally, it has been shown that if existing brand advertising programs are changed as a result of a generic advertising program, the required minimum generic advertising response for farmers to gain would be changed. Whether such changes would occur and in which direction and by how much depends very much on the form of the strategic games being played by the processors and retailers in any particular market. However, to our knowledge, no published study of the advertising of agricultural products has considered estimating the strategic reactions of brand advertising to changes in the level of generic advertising.

7. References

Alston, J, Sexton, R and Zhang, M (1997), “The effects of imperfect competition on the size and distribution of research benefits”, American Journal of Agricultural Economics 79, 1252-1265.

Australian Parliament (1999), Report of the Joint Select Committee on the Retailing Sector, Canberra.

Ball, K and Dewbre, J (1989), An Analysis of the Returns to Generic Advertising of Beef, Lamb and Pork, Australian Bureau of Agricultural Economics Discussion Paper No.4, Australian Government Publishing Service, Canberra.

Cotterill, R (2000), Dynamic Explanations of Industry Structure and Performance, Food Marketing Research Centre, Research Report No. 53, Department of Agricultural and Resource Economics, University of Connecticut.

Cotterill, R, Putsis, W and Dhar, R (2000), “Assessing the competitive interaction between private labels and national brands”, The Journal of Business 73(1), 109-131.

Cranfield, J (1996), "Advertising and Oligopoly Power in the North American Beef Industry”, unpublished M.Sc. thesis, Department of Agricultural Economics and Business, University of Guelph.

Cranfield, J and Goddard, E (1999), “Open economy and processor oligopoly power effects of beer advertising in Canada”, Canadian Journal of Agricultural Economics 57, 1-9.

Dhar, T and Cotterill, R (2002), Price Transmission in Differentiated Market Channels, Food Marketing Research Centre, Research Report No. 67, Department of Agricultural and Resource Economics, University of Connecticut.

Dixon, P and Rimmer, M (2002), Dynamic General Equilibrium Modelling for Forecasting and Policy, North-Holland, Amsterdam.

Duffy, R (1995) 'The Benefits to Canadian Hog Producers of Generic vs. Branded Advertising of Pork.' MSc thesis, Department of Agricultural Economics and Business, University of Guelph.

Eales, J and Brinkley, J (2003), “Vertical product differentiation in theory and practice”, Journal of Agricultural & Food Industrial Organisation, 1, article 16.

Freebairn, J and Alston, J (2001), “Generic advertising without supply control”, Australian Journal of Agricultural and Resource Economics 45(1), 117-146.

Funk, T, Meilke, KD and Huff, H (1977), 'The effects of retail pricing and advertising on fresh beef sales', American Journal of Agricultural Economics 59, 533-537.

Goddard, EW and Griffith, GR (1992), The Impact of Advertising on Meat Consumption in Australia and Canada, New South Wales Department of Agriculture, Research Workpaper Series 2/92, Armidale.

Holloway, G (1991), “The farm retail price spread in an imperfectly competitive food industry”, American Journal of Agricultural Economics 73, 979-989.

Hoover, S, Hayenga, M and Johnson, SR (1992), 'Evaluating the effectiveness of generic pork advertising: the first fifteen months', in Commodity Advertising and Promotions, (H Kinnucan, SR Thompson and HS Chang, eds), Ames, Iowa: Iowa State University Press.

Jensen, H and Schroeter, JR (1992), 'Television advertising and beef demand: an econometric analysis of split cable household panel scanner data’, Canadian Journal of Agricultural Economics 4(2), 271-294.

Kadiyali, V, Vilcassin, N and Chintagunta, P (1996), “Empirical analysis of competitive product line pricing decisions: lead, follow, or move together”, The Journal of Business 69(4), 459-487.

King, S and Maddock, R (1996), Unlocking the Infrastructure: The Reform of Public Utilities in Australia, Allen and Unwin, St. Leonards.

Kinnucan, H (1999), “Advertising traded goods”, Journal of Agricultural and Resource Economics 24, 38-56.

Kinnucan, H (2003), “Optimal generic advertising in an imperfectly competitive food industry with variable proportions”, Agricultural Economics 23, 143-158.

Kinnucan, H and Myrland, O (2000), “Optimal advertising levies with application to the Norway-EU Salmon Agreement”, European Review of Agricultural Economics 27, 39-57.

Mounter, SW, Griffith, GR and Piggott, RR (2005), "The payoff from generic advertising by the Australian pig industry, in the presence of trade", Australasian Agribusiness Review, Volume 13, Paper 4 (listed February 22, 2005). Available at http://www.agrifood.info/Publications_Review/Mounter_Griffith_Piggott.htm

Muth, MK and Wohlgenant, MK (1999), "A test for market power using marginal input and output prices with application to the US beef processing industry", American Journal of Agricultural Economics 81(3), 638-643.

O'Donnell, CJ, Griffith, GR, Nightingale, JJ and Piggott, RR (2005), Food Processor/Retailer Market Power in Input Markets: The Australian Grains and Oilseeds Industries, Final Report to the Rural Industries Research and Development Corporation on Project UNE-79A, RIRDC Publication No. 05/019, Canberra, April.

Piggott, NE, Chalfant, JA, Alston, JM and Griffith, GR (1996), "Demand response to advertising in the Australian meat industry", American Journal of Agricultural Economics 78(2), 268-279.

Putsis, W and Dhar, R (1998), “The many faces of competition”, Marketing Letters 9(3), 269-284.

Quilkey, J (1986), “Promotion of primary products - a view from the cloister”, Australian Journal of Agricultural Economics 30, 36-52.

Sellen, D, Goddard, E and Duff, S (1997), 'Returns from research and advertising in the North American hog and pork industry', in Economic Analysis of Research and Promotion: Proceedings from the Symposium Sponsored by NC-208 and NEC-63, New Orleans, Louisiana, March 21-22.

Sexton, R (2000), “Industrialisation and consolidation in the US food sector: implications for competition and welfare”, American Journal of Agricultural Economics 82, 1087-1104.

Shank, B, Goddard, EW, Freebairn, JW and Griffith, GR (2004), “Econometric modelling of the market for shell eggs in supermarkets in Australia”, Chapter 4 in Optimal Egg Marketing Under Changing Market Structures, Final Report to the Australian Egg Corporation Limited on Project UM-61A, University of Melbourne, Parkville, August.

Ward, RW and Lambert, C (1993), 'Generic promotion of beef: measuring the impact of the US beef checkoff', Journal of Agricultural Economics 44, 456-465.

Wohlgenant, M (1993), “Distribution of gains from research and promotion in multistage production systems: the case of the US beef and pork industries”, American Journal of Agricultural Economics 75, 642-651.

Wohlgenant, M and Piggott, N (2003), “Distribution of gains from research and promotion in the presence of market power”, Agribusiness 19(3), 301-314.

Zhang, M and Sexton, R (2002), “Optimal commodity promotion when downstream markets are imperfectly competitive”, American Journal of agricultural Economics 84(2), 352-365.

Zhao, X, Mullen, J, Griffith, G, Piggott, R and Griffith, W (2003), “The incidence of gains and taxes associated with R&D and promotion in the Australian beef industry”, Agribusiness 19(3), 333-344.

Zhao, X, Mullen, JD, Griffith, GR, Griffiths, WE and Piggott, RR (2000), An Equilibrium Displacement Model of the Australian Beef Industry, Economics Research Report No. 4, NSW Agriculture, Orange, December. Available online at: http://www.agric.nsw.gov.au/reader/16031.