Efficiency Measurement of Australian Dairy Farms: National and Regional Performance

Iain Fraser and Mary Graham

 

---

Abstract

In this paper we use Data Envelopment Analysis (DEA) to estimate technical efficiency for a sample of 1742 Australian dairy farms. Bearing in mind data limitations we find that average technical efficiency is 59 per cent, but there are significant regional differences. These results reflect differences in State level milk marketing arrangements in place before dairy deregulation in July 2000 providing an ex post explanation for the changing composition of dairy farms in Australia. We also examine two important technical aspects of DEA implementation. First, how changes in model input specification alter the relative performance of farms. Second, we employ a simple bootstrap procedure to show how changes in sample size affects estimates of technical efficiency. These results have simple but important implications for the use of DEA as an industry-benchmarking tool.

Key Words: Dairy farms, DEA, regions, bootstrapping.

1.         Introduction

The dairy industry in Australia is a major industry in terms of the value of production, employment and as well as an important source of exports. With an estimated gross value of production of nearly $3 billion a year, dairy ranks third behind wheat and beef in terms of output value at the farm gate. At the farm level ABARE (2001) reports that since the mid-1970s, milk production has more than doubled. Increased farm and herd size, combined with increased milk yield per cow, have resulted in a 160 per cent increase in milk production per farm.

The pressures on dairy farmers industry to remain efficient have increased following deregulation of the industry in July 2000, and the introduction of a competitive market structure (Edwards, 2003). These changes follow on from significant deregulation earlier to the dairy processing industry that lead to dairy farms being exposed directly to world market forces (Doucouliagos and Hone, 2000).

Research on the effects of deregulation indicate that dairy farmers in several states will be operating in far less favourable conditions (ACCC, 2001), particularly farmers in Queensland, New South Wales and Western Australian. Subsequently, research by Ashton and Spencer (2002) has found that since June 2000 the number of registered dairy farms has fallen significantly in New South Wales (17 per cent), Queensland (16 per cent) and Western Australia (13 per cent). In contrast, Victoria, which was forecast to fair better as a result of deregulation, has only experienced a reduction of 3 per cent.

The reason for the changes in farm numbers can in part be traced back to the structure of milk marketing arrangements in the States prior to deregulation. It can be conjectured that the States milk marketing arrangements provided different economic signals that gave rise to differing degrees of farm level efficiency across the States. This implies that the response we have observed since deregulation is the less efficient farms departing and that more of these farms were located in States that operated relatively more inefficient milk marketing policies. If this were the case we would expect to see some evidence of regional differences in dairy farm level efficiency prior to deregulation.

In this paper we examine this conjecture by estimating technical efficiency for a large sample of Australian dairy farms drawn from all of the main dairy producing regions. To undertake our analysis we employ Data Envelopment Analysis (DEA), a mathematical programme technique, developed by Farrell (1957) (See Coelli et al., 1998, for more details). DEA has been used in a number of previous papers to examine technical efficiency of dairy farms e.g., Weersink et.al. (1990), Cloutier and Rowley (1993), Jaforullah and Whiteman (1999), and Fraser and Cordina (1999). Like the antecedent literature we estimate technical efficiency and scale efficiency for our sample of farms. We also consider how the choice of inputs to describe production affects our efficiency estimates.

In addition, because of the large size of our sample we are able to consider two important issues relating to the implementation and interpretation of DEA.  First, we examine how estimates of technical efficiency change when employing the whole sample as opposed to regional sub-samples.  The differences we identify stem from the influence of sample size on DEA estimates of efficiency. Second, we employ a simple bootstrap procedure, introduced by Zhang and Bartels (1998), to correct for differences in sample size. We employ this procedure when estimating efficiency for each dairy region separately allowing us to take account of differences in sample size to ensure comparable results across the regions in terms of potential increases in efficiency within a region.

The structure of this paper is as follows. In section 2 we describe DEA used to undertake the analysis and review existing DEA applications to dairy farms. We then describe the survey and the data set used in the analysis. In Section 4 we present our results. The results are divided into two parts. First, we present those that deal with the whole data set, i.e., the national level. Second, we present results for the various dairy regions. Finally, in Section 5 we present conclusions.

2.         Data Envelopment Analysis

2.1 Method

DEA is based on a linear programming specification and is used to estimate a production frontier so that from observed data, the efficiency of an economic unit (i.e., a farm) can be measured (Farrell, 1957 and Charnes et al. 1978). A production frontier that envelops all the data is estimated with observations lying on the production frontier defined as technically efficient (TE). Those observations that lie below the frontier are considered inefficient. A relative measure, the TE of a farm relative to others in the sample, is derived. TE measures by how much each input can be radially reduced (or output increased) to produce an efficient outcome.

TE can be decomposed to determine the contribution of pure technical factors (PTE) and scale efficiency (SE) to the overall level of efficiency. To obtain separate estimates of PTE and SE, input orientated technical efficiency measures satisfying three different types of scale behaviour are specified. These are constant returns to scale, (CRS), variable returns to scale (VRS), and non-increasing returns to scale (NRS).

The first linear program we specify and estimate is an input orientation model assuming CRS (Charnes, et al, 1978). The linear program we estimate is as follows:

min_qlq

subject to         

Yl - y_i ³0

q x_i - Xl ³0

            l ³ 0                                                                             (1)

where we assume that we have K inputs, M outputs, N farms and that x_i and y_i are the inputs and outputs for the i-th farm. X is K by N input matrix, Y is an M by N output matrix, q is a scalar and l is a N * 1 vector of constants. 

The value of q estimated will be the efficiency score of the i-th farm. It will satisfy the condition q£1, with a value of 1 indicating a point on the production frontier and thus a TE farm. A value less than one indicates the farm, given the set of observations in the sample, can improve the efficiency of its inputs by forming benchmarking partnerships and emulating the best practices of its reference or peer group of farms. To derive a set of N TE scores, the problem needs to be solved N times, once for each farm.[1]

The CRS specification assumes that all farms are operating at optimal scale. However, scale inefficiency may arise from a number of factors. To measure inefficiencies due to scale, and to identify the optimal scale for a farm, two more DEA models need to be solved. These are the VRS and NRS model specifications.

Estimating a VRS specification allows TE to be estimated without the influence of SE. To estimate the VRS specification, an additional convexity constraint, N1’l, is added to the programming problem (1) above, and N1 is an N by 1 vector of ones. The VRS specification forms a production frontier that envelopes data more closely than the CRS specification. Therefore, the resulting efficiency scores are equal to or greater than those obtained with the CRS model. The additional convexity constraint ensures that an inefficient farm is only being compared against farms of similar size. Thus, by estimating both CRS and VRS specifications, TE estimates can be decomposed into two components, PTE and SE. If there is a difference between the CRS and VRS TE scores, this indicates scale inefficiencies exist.

Assuming a farm is scale inefficient, in order to assess if it is exhibiting increasing or decreasing returns to scale (IRS/DRS), a non-increasing returns to scale (NIRS) specification is required to be estimated. The NIRS specification adjusts the restriction N1’l=1, such that N1’l£ 1. This constraint ensures that farms will only be compared to farms of the same or smaller size, not with any farm that is larger. To determine if IRS and DRS exists, the NIRS TE is compared to the VRS TE estimate. If the two are unequal, then this indicates IRS and the scale of farm level operations can be increased. If the two are equal, DRS exists and farm operations needs to be reduced in size.

2.2        Existing DEA Applications

DEA has been used to examine efficiency in many industries in many countries (Coelli, et al., 1998). There have also been a number of applications of DEA to dairy farming both in Australia and overseas. For example, Weersink et al. (1990), employed DEA to analyse technical efficiency for a sample of 105 Ontario, Canada, dairy farms. Various measures of farm level efficiency were estimated and analysed. Analysis found that a majority of the dairy farms were efficient, and that overall efficiency increased with herd size. Scale efficient farms were found to exist under a variety of herd sizes. He concluded that competitive pressure might continue the trend towards larger farms although the variation in optimal scale between herd sizes implied a range of farm sizes might continue to exist, provided appropriate technology for the scale of production is chosen. Another Canadian study, Cloutier and Rowley (1993), considered technical efficiency of 187 dairy farms in Quebec, over a two year period. Using a CRS specification, they found more efficient farms in 1989 than in 1988. Cloutier and Rowley suggest that their results indicate that larger farms are much more likely to appear efficient than smaller ones. However, they performed no statistical tests to see if the differences were significant.

Jaforullah and Whiteman (1999) analysed scale efficiency in the New Zealand dairy industry with a sample of 264 farms for 1993. They found average technical efficiency high at 89 per cent.  In terms of returns to scale, they found more farms operating at below optimal scale, and concluded that the trend towards larger farms should be encouraged to increase the productive efficiency of the farms. However, the study did not clarify if farms were drawn from a homogeneous geographical region and given the large variation in soil and weather in New Zealand, it was not clear if important exogenous factors had been accounted for satisfactorily.

Fraser and Cordina (1999) assessed the technical efficiency of a sample of 50 irrigated dairy farms in Northern Victoria, Australia, with data collected over the 1994/5 and 1995/6 lactation periods. Both CRS and VRS input orientation models were specified to estimate technical efficiency. From the sample of farms analysed, it was found that a significant number were operating, or were very close to operating, efficiently. Although the analysis did not consider the reasons why particular farms were efficient and others were not, there is unlikely to be much variation in the production technology used. Socio-economic characteristics and their significance to technical efficiency were felt to be worthy of further study.

In relation to the existing literature the current study makes three related contributions. First, our study applies DEA to a much larger sample of farms than previously used. The influence of sample size on DEA estimates of efficiency is well understood. Simar and Wilson (2000) note that DEA estimates of efficiency approach the “true” measures of efficiency for a sample of data as the sample size increases. As noted, the size of the sample used in this study is significantly larger than used in previous research.

On a related point Zhang and Bartels (1998) demonstrated that estimates of efficiency decrease as the number of firms or farms in a sample increase. Given the size of the sample employed in this study we can examine this issue from an industry perspective. Finally, the size of our sample means that we are not constrained as to the number of variables we use in our analysis.  Chambers et al. (1998) suggest that any farm level DEA study should be based on a sample that has at least three times as many farms as there are inputs.  Clearly, this is not a constraint on the current study.

Second, our sample data allows us to perform efficiency analysis at the national and regional levels. This means we can examine how sample size affects efficiency estimates, and also it allows us to examine the relationship between farm level efficiency estimates derived from two samples; one where the data is drawn entirely from within a single dairy region, and the second where the data is from the national sample. As indicated, Jaforullah and Whiteman (1999) used data drawn from all regions of New Zealand but they did not examine how important regional differences were on the results generated. Recent research by ABARE (2001) of the Australian dairy industry also tends to overlook the issue of regional aggregation of data.

Third, we examine how the choice of variables used in the analysis can affect the results generated. In particular we focus on irrigation. The reason for focusing on irrigation is that recent research on the Australian dairy industry by ABARE (2001) appears to have overlooked this input in its assessment of regional productivity.  We examine how the inclusion/exclusion of a key input in pasture production affects the results generated.

3.         Data Source and Description

As part of the Dairying For Tomorrow project, a nationwide survey of dairy farm management practices and productivity was conducted by an independent research organisation, IRIS Research, on behalf of the Dairy Research Development Corporation (DRDC) in 2000. A 30 minute telephone survey to over 1800 farmers throughout Australia, over a six month period, had a response rate of 84 per cent. The results of this survey, made available by the DRDC, are used in this paper to examine the level of efficiency in the industry. Of the 1826 farmers interviewed, 84 have been deleted due to incomplete data, leaving a sample of 1742.

The data draws on all dairy regions of Australia. The data is divided into eight regions, grouped according to the DRDC regional development programs. The eight regions are: i) Sub-Tropical in eastern Queensland; ii) DIDCO in the central coastal area of New South Wales; iii) Murray in the River Murray region of Victoria and New South Wales; iv) Gipps in eastern Victoria; v) WestVic in south-west Victoria and south east of South Australia; vi) Tas in Tasmania; vii) Dairy SA in South Australia; and viii) Western in south-west Western Australia.

As in previous studies we employ a single output measure. Dairy farm production can be measured in terms of litres of milk, or kilograms of butterfat. Measures of butterfat were converted into a common output measure of litres of milk. Thus, in this analysis, the output measure used is litres of milk.

Although the survey can be claimed to be extensive in terms of its Australian wide coverage, it did have data limitations, particularly with respect to data on inputs. Significantly, no labour data was reported and the only measure of capital value reported was based on the farmer’s estimate. The exclusion of a labour variable (estimated to be 18 percent of input costs by ABARE, 2002) will bias our results to a certain extent and needs to be borne in mind when interpreting the findings. In addition, while the authors accept the farmer’s own assessment of the value of capital could be highly subjective and subjective to error, no other measure was reported.

In terms of inputs we constructed six from the survey. First, we took information on various forms of feed to construct a measure of purchased feed. Second, the size of the farm was gauged from the size of the milking area, in hectares. Third, herd survey was taken as the number of milking cows. Fourth, as a measure of water use, data relating to irrigation was examined. Many of the farms using irrigation did not give details on the number of megalitres used. To gain a larger response rate, the data relating to area of the farm irrigated, in hectares, was used as a proxy. This refers to the area to which irrigation water was applied, thus excluding rainfall and re-use systems. Fifth, from a number of questions asked on the use of different types of fertilizers and how decisions on the application of fertilizers were made, we were able to construct a measure of fertiliser use. Sixth, as discussed above, the farmer’s estimate of the value of the farm was used as a measure of capital.[2]

A summary of the data used in the analysis is presented in Table 1.

Table 1:  Descriptive Statistics by Region

	Dairy SA	Tasmania	DIDCO	Gipps	Murray	Sub-Tropical	WestVic	Western
Number of farms	130	179	191	295	308	265	280	94
Milk Output (000’s megalitres) Mean Min Max	1,029 70 5,000	896 103 4,300	807 115 4,000	876 118 5,500	993 80 9,000	578 80 2,200	1,168 900 7,500	1,190 314 4,500
Hectares Mean Min Max	147.1 12 1497	112.3 20 465	103.2 20 486	98.1 20 526	116.5 16 607	140.8 16 898	145.8 30 1300	206.5 51 800
Cow Numbers Mean Min Max	182 22 730	219 32 250	156 40 750	200 36 1150	204 38 1600	138 30 600	237 30 1300	207 60 800
Feed ($per cow) Mean Min Max	2.06 0 12.5	0.49 0 5.78	1.67 0 8.0	0.83 0 5.78	1.38 0 5.56	1.32 0 12.6	1.2 0 5.05	1.61 0 8.3
Irrigation (hecs) Mean Min Max	43.28 2 263	44.3 4 243	41 4 162	70.3 4 405	92.3 4 668	28.8 4 243	44.1 2 280	43.34 12 101
Fertilizer(000’s $) Mean	14	25	17	17	15	13	24	26
Capital (000’s $) Mean	1,021	815	1,073	845	901	823	801	1,588

Table 1 shows that individual dairy regions differ in terms of quantity of milk produced as well as the production technology and mix of inputs used. Western region had the highest average megalitres of milk output, just ahead of WestVic and Dairy SA, with Sub-Tropical the lowest. Average farm size varied from 98 hectares in Gipps to 206.5 hectares in Western. Cow numbers were more consistent, with five regions having an average of more than 200. The higher irrigation regions, namely Murray and Gipps, had much lower fertilizer expenditure compared to Tasmania and WestVic. The use of supplementary feed was significant for all regions except Tasmania. The capital value of the farms varied across the regions, from a high of $1,587,766 in Western to $815,643 in Tasmania.

4.         Results

Our results are presented in the following order. First, we present TE estimates for the whole sample set assuming CRS. This allows us to examine the relative performance of all dairy regions. We also present TE results including and excluding irrigation to illustrate how the choice of variables used in the analysis affects the efficiency estimates derived. Second, we estimate CRS TE for each region individually. We correct these estimates for differences in sample size following Zhang and Bartels (1998) by employing bootstrapping. Third, VRS results are presented for each region so that farms operating at constant, increasing, and decreasing returns to scale can be identified and the optimal scale of production (i.e., by herd size) for each region determined.

4.1        Whole Sample CRS

4.1.1     Irrigation Input Included

Employing a CRS specification for the whole sample we found that sixty-three (63) or 3.6 per cent of the farms were regarded as being TE (q = 1). The distribution of mean TE estimates is illustrated in Figure 1 and summary statistics reported in Table 2.

Table 2: Statistical Summary: Technical Efficiency (6 inputs) Australia and Regions

Region	Australia	Dairy SA	Tasmania	DIDCO	Gipps	Murray	Sub-Trop	West Vic	Western
No.Farms	1742	130	179	191	295	308	265	280	94
Mean	0.589	0.622	0.603	0.573	0.614	0.578	0.521	0.614	0.625
Minimum	0.131	0.17	0.252	0.228	0.221	0.131	0.148	0.215	0.253
Maximum	1	1	1	1	1	1	1	1	1

 

Figure 1:  Farm Level Efficiency:  All Australia

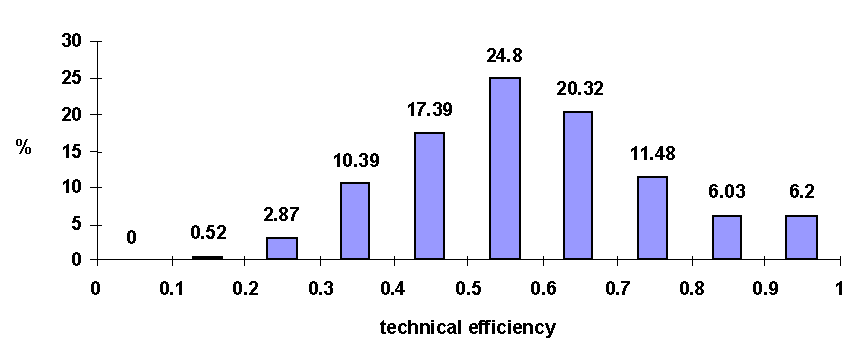
Figure 1 shows that the distribution of average TE is almost normal in shape. The average estimate of TE is 0.59. Half the farms in the sample had a TE of between 0.47 and 0.69. The least efficient farm with an estimate of 0.131 is in the Murray region. For this farm, inputs consumed could be reduced by 86.9 per cent without any reduction in output. 

The average level of TE in this study is much lower than found in other studies, both in Australia and overseas, and is a reflection of the size of the sample used. Fraser and Cordina (1999) sample of 50 farms in northern Victoria had an average efficiency of 0.86 over a two-year period. This is comparable to overseas studies in New Zealand and Canada where farms had an average efficiency of 0.83 to 0.92 respectively (see Jaforullah and Whiteman, 1999, Cloutier and Rowley, 1993, and Weersink et al., 1990).

Table 2 also provides a regional breakdown of the results. The best performing regions, that is, those regions whose mean level of efficiency is above the national average are Gipps, WestVic, Tasmania, Dairy SA and Western. Western with a mean of 0.625 was the best performer. The remaining three regions, Sub-Tropical, Murray and DIDCO were the poorer performers. These results support the conjecture that Queensland and New South Wales milk marketing arrangements prior to deregulation in 2000 gave rise to less efficient dairy production relative to other regions of Australia.

4.1.2     Irrigation Input Excluded

Performance evaluation of dairy farms over all Australia brings in many variables that differ considerably across the nation. Climatic conditions differ widely and produce different reliance on, for example, the need to irrigate, or the need to introduce supplementary feeding. The production technologies adopted by farms reflect such regional differences. For example, Table 1 reports differences in the extent of irrigation use. In the Murray region, where approximately 80 per cent of the farms irrigate, an average of 92 hectares per farm is irrigated, while in Sub-Tropical, where only 21 per cent of the farms irrigate, an average of 29 hectares per farm is irrigated. Grouping all the regions together to examine the efficiency of Australian dairy farms, gives no recognition to such regional differences. If, for example, irrigation is included as an input in the model estimated, the efficiency results obtained will be biased in favour of those farms that do not need to rely on irrigation.

To highlight the importance of model specification we repeat the same analysis i.e., CRS for whole sample, but we only employ five inputs, leaving out irrigation. This analysis illustrates a potential weakness in DEA analysis if insufficient detail is paid to the mix of farms and farm systems included within a sample.  Statistical summaries are presented in Table 3.

Table 3: Statistical Summary Technical Efficiency (5 inputs):  Australia and Regions

Region	Australia	Dairy SA	Tasmania	DIDCO	Gipps	Murray	Sub-Trop	West Vic	Western
No.Farms	1742	130	179	191	295	308	265	280	94
Mean	0.530	0.581	0.545	0.511	0.536	0.563	0.475	0.533	0.493
Minimum	0.131	0.17	0.222	0.165	0.189	0.131	0.142	0.213	0.238
Maximum	1	1	1	1	1	1	1	1	0.845

As shown in Table 3 the range of TE is between 0.131 to 1, but with a slightly lower mean of 0.53 compared to the six input model specification. All dairy regions have a lower level of TE, but some show much greater changes. Western, the best performer with six inputs now ranks seventh as a result of TE dropping 14 per cent from 0.63 to 0.49. Murray rises from being ranked sixth to being second behind Dairy SA. The farms in Dairy SA and Murray showed greater consistency in both analyses than did farms in any other region. 

The reason for this result is obvious. The output of farms reflects inputs used, including for most farms in the Murray region, irrigation. These farms have the same output whether or not irrigation is included as an input in the model. Since most farms have a value for the irrigation input, their TE estimate does not vary much when irrigation is excluded. The farms that have lower TE efficiency are those that do not irrigate.

4.1.3     Comparing Model Specifications

A simple way to compare the impact of model specification is to examine the performance of best and worst performing farms by region.  Table 4 summarizes the performance of the top and bottom 50 farms in each region, with and without irrigation as an input in the model. 

Table 4: Distribution of Efficient/Inefficient Farms by Region - Number (Percentage)

The analysis shows that all regions suffered a decrease in the number of fully efficient farms when irrigation was excluded. The proportion of fully efficient farms fell from 3.6 per cent (63 farms), to 2.2 per cent (38 farms). A closer examination of the regions in terms of the fully efficient and the least efficient farms reveals the importance of selecting the correct inputs for the analysis. Tasmania and the Sub-Tropical regions both lost six efficient farms, but only one in Tasmania remained outside the top 50 farms. The Sub-Tropical region experienced significant changes, with four previously fully efficient farms remaining outside the top 50 farms, and one experiencing a fall to 0.35 and another to 0.65. The top regional performer, Western, had no fully TE farms, the top performer achieving only 0.85 efficiency.

Although these changes appear to be significant it is necessary to statistically test the results. A Spearman Rank Correlation Coefficient, (SRCC) is estimated as a statistical check on the consistency of two model specifications in terms of in the relative ranking of the farms. The SRCC statistically tests if the relative rank of farms changes when employing the different model specifications.  The SRCC test statistic is calculated as follows:

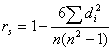                                                                                                        (2)

where d_i is the difference between the rankings for each observation (i.e., farm) under the different model specifications and n is the sample size. [3]

The hypothesis tested is:

H₀: r_s = 0; there is no relationship between the model specifications

H₁: r_s ¹ 0; there is a relationship between the model specifications

With n>30, r_s is approximately normally distributed with mean zero and standard deviation 1/(n-1)^0.5, so that the Z test is Z = r_s(n-1)^0.5. An SRCC estimate of 0.88 was obtained allowing us to reject the null hypothesis indicating that a strong positive statistically significant correlation exists between the TE estimates obtained by the two models. Thus, the ranking of farms is statistically invariant to the model specifications examined here.

In aggregate, with the data and models examined here model specification has little impact on the best and poorest performers. There is one notable exception, the Western region, whose overall performance and ranking relative to the other dairy regions changes significantly. But, statistically the results produced by either specification in terms of the rank of farms is the same.

4.2.       Regional Analysis

To take account of differences in regional production technologies and variables, many of which are beyond the control of farmers, we now undertake efficiency analysis for each individual region. This means that farms will then only be compared to farms operating within the same region.  Hence, the results allow us to measure how much within region TE could be increased. However, we do not consider it appropriate to directly compare differences in TE between the regions because in this analysis we are assuming that regional production technologies are different. To make a meaningful region-by-region comparison it is necessary to assume that the production technology is the same across regions and if this is the case we can consider regions in the same sample. Thus, the results presented for the whole sample provide the most consistent estimates of the relative performance of the eight dairy regions in Australia. [4]  

In this section we present two sets of CRS TE results. First, we estimate TE for each region using all data assuming five and six inputs. Second, we follow Zhang and Bartels (1998) and employ a simple bootstrap procedure to take account of differences in sample size between regions.  They illustrated the importance of the bootstrap procedure using Monte Carlo simulations that as the number of firms increases in a sample the estimates of TE fall. We undertake this procedure so that we produce a consistent estimate of the potential increase in TE within a region compared to all other regions.

The Zhang and Bartels (1998) bootstrap procedure is very simple.

1. Decide on the size of the sub-sample of farms to be drawn. Given that Western is the smallest sample (n=94) we have set the bootstrap sub-sample at n=94. The sub-sample of farms is drawn without replacement from the region sample. 
2. The sub-sample of farms is then used to estimate a sample-adjusted measure of TE.
3. This procedure is repeated 1,000 times to yield an average sample-adjusted measure of TE. 

We employ the bootstrap procedure with the five input model specification. All results are presented in Table 5.

Table 5:  TE Analysis of Individual Dairy Regions - 6 Inputs, 5 Inputs and Bootstrap

	Dairy  SA	Tasmania	DIDCO	Gipps	Murray	Sub-Trop	WestVic	Western
No. Farms	130	179	191	295	308	265	280	94
Average TE  (6 inputs)	0.794	0.722	0.729	0.705	0.729	0.638	0.737	0.822
Average TE (5 inputs) Bootstrap* Adjusted Average TE (5 inputs)	0.720 0.789 (0.069)	0.655 0.771 (0.116)	0.662 0.817 (0.155)	0.675 0.814 (0.139)	0.693 0.796 (0.103)	0.626 0.719 (0.093)	0.680 0.725 (0.045)	0.817 0.817 (0.000)

* The number in the bracket is the difference between the adjusted and unadjusted average TE

The results in Table 5 reveal several interesting issues. First, the TE estimates for all regions for both five and six inputs are significantly higher compared to the TE estimates for the whole sample.  This result is important. It clearly illustrates the relative nature TE estimates derived using DEA.  Second, as demonstrated earlier, moving from a six to five input model specification reduces TE estimates in all regions.

Third, the bootstrap results show that for all regions, except Western which is the sample size of the bootstrap procedure, when we take account of differences in sample size TE estimates increase. That is, the adjusted bootstrap estimates are all much closer than indicated by unadjusted analysis. In terms of a region-by-region analysis Western still has the highest level of average TE but it is now equal with DIDCO. These results mean that for the prevailing dairy production technology in these regions that input use could be reduced by approximately 18 per cent.  Also the Sub-Tropical region has the lowest average level of TE implying that the average farm in this region has more to gain from attaining best practice compared to all other regions.

Fourth, the bootstrap results indicate that there is a non-monotonic relationship for the regions between the increase in adjusted TE and unadjusted TE and sample size.  For example, DIDCO has a sample of 191 farms, which is by no means the largest, but it does experience the biggest increase when adjusting TE. The variation in the results highlights the fact that the underlying distribution of TE differs between regions and that this impacts on the bootstrap results.

4.3.       Optimal Scale of Production

We now present results examining optimal scale of production. We estimate VRS and NIRS DEA specifications in all regions, so that IRS, CRS and DRS can be identified. We then match herd size with those farms operating at CRS within in each region so that the optimal scale of production can be determined. Table 6 presents SE results for all regions.

Table 6: Optimal Scale of Production (CRS) (%) and Optimal Herd Size

Dairy Region	CRS	IRS	DRS	Mean Herd size CRS farms	Herd increase on region average
Dairy SA	26.2	69.9	3.9	224	42
Tasmania	22.4	68.1	9.5	268	49
DIDCO	15.7	76.4	7.9	211	81
Gipps	15.3	76.6	8.1	271	71
Murray	14.3	65.6	20.1	241	37
Sub-Tropical	14.3	78.5	7.2	204	66
WestVic	17.8	73.2	8.9	272	35
Western	22.3	69.2	8.5	286	79

In keeping with previous results in the literature (e.g., Weersink et.al., 1990, Jaforullah and Whiteman, 1999, and Fraser and Cordina, 1999) few farms in any region are operating at DRS.  Farms generally are not too big. The only exception is the Murray region where 20% of farms were operating at DRS.

In all regions, upward of 65 per cent of farms could improve SE if they increased scale in terms of land or herd size, for example. Using herd size as a measure of scale, the optimal scale of production for each region is determined. The fourth column in Table 6 indicates average herd size of farms within a region operating at CRS.  The fifth column shows by how much average herd size needs to be increased within each region if all farms operated at CRS. These results indicate that the potential increase in herd size is high in many regions, especially DIDCO and Western.

We can see from these results that there are significant differences in the scale of operation as measured by herd size across the regions of Australia. Sub-Tropical has the smallest average herd size with 204 and Western the largest at 286. Although each region has a different optimal herd size the analysis does suggest two distinct groupings of dairy regions: 200-220 cows; and 270 plus. Only the Murray region has a herd size in-between. Thus, although the competitive pressure brought about by the deregulation of milk marketing will continue to pressure farms to grow larger, there are important regional differences in optimal target herd size. Whether these regional differences will remain, as the market for milk continues to adjust as a result of deregulation, is a question that requires further research.

5.          Conclusion

This paper has employed DEA to measure TE and SE for a large sample of Australian dairy farms. Our results provide ex post support for the view that inherent inefficiency in milk production as a result of prevailing milk marketing structures would mean that dairy deregulation in 2000 would have a greater impact on dairy farming in Queensland and New South Wales than compared to Victoria. Thus, the differences we identify in TE between the regions when we assume that there exists a common production technology and prevailing institutional and environmental factors, is in keeping with our prior expectations.  However, regardless of the model estimated, there are a large number of efficient farms, but there are also many, across all eight dairy regions, who are technically inefficient and whose output could be increased without changing the level of their input use.

Specifically, our results also indicated that only minor variations in TE occur when we adjust model specification. We examined how the inclusion/exclusion of irrigation affected TE estimates.  Our SRCC estimates provide statistical support for the robustness of the TE estimates under either models specification. That is, the relative rank in terms of the TE estimate for a farm is invariant to the model specification.

When using the whole data set, estimates of TE are derived from comparing farms drawn from different climatic and physical conditions as well assuming a common production technology. To take account of the regional differences we re-estimated TE for each of the eight dairy regions individually. The analysis revealed several important results. First, the size of the sample impacts upon the TE estimates obtained. Reducing the sample size and examining regions individually improves the overall performance of both a region and farms with the region i.e., they have higher TE. However, within region analysis means that farms are being compared to farms that are far more likely to be facing similar climatic and geological factors. Second, only by adjusting sample size following the bootstrap procedure of Zhang and Bartels (1998) can we ascertain by how much TE within each region can potentially increase compared to other regions.

We have also found that many farms across all regions are operating at below the optimal scale of production. In terms of herd sizes, all regions could increase their scale of operation, although just how large the herds should be varies between the regions. This variation in optimal scale between herd sizes suggests that a range of farm sizes may well continue to exist across all dairy regions.

Finally, in this paper efficiency has only been examined in relation to TE and SE. No cost data has been considered or a measure of labour use. As we previously acknowledge the lack of labour use data means that the results presented here do need to be treated with some degree of caution. Furthermore, many socio-economic factors such as farmer age, level of education, and off farm employment may also account for differences in efficiency we find. Previous research has found that age and educational level impact on technical efficiency (Kumbhakar et al., 1991, and Tauer and Siefanades, 1998). We have also ignored the environmental impact of dairy farming that may become more important in terms of efficiency of operation. For example, to what degree does efficiency levels impact on sound environmental practices such as waste handling? These issues remain an area for future research.

Acknowledgments

The authors would like to thank DRDC for making the data available and Paul Kim for helping with the GAUSS code used to run the bootstrap analysis.

References

ABARE (Australian Bureau of Agricultural and Resource Economics) (2001), ‘Australia's Expanding Dairy Industry: Productivity and Profit’, Canberra

ABARE  (Australian Bureau of Agricultural and Resource Economics)  (2002), Production, Efficiency and Productivity of Australian Dairy Farms. Report to DRDC.

ACCC (Australian Competition and Consumer Commission) (2001), ‘Impact of Farmgate Deregulation on the Australian Milk Industry’, Monitoring Report, Canberra.

Ashton, D and Spencer, D. (2002), Dairy: Outlook for 2006-07, Australian Commodities, 9, 63-69.

Chambers, R.G., Fare, R., Jaenicke, E. and Lichtenberg, E. (1998), Using Dominance in Forming Bounds on DEA Models: The Case of Experimental Agricultural Data, Journal of Econometrics, 85, 189-203.

Charnes, A., Cooper, W.W. and Rhodes, E. (1978), Measuring the Efficiency of Decision Making Units, European Journal of Operational Research, 2, 429-444.

Cloutier, L. M. and Rowley, R. (1993), Relative Technical Efficiency:  Data Envelopment Analysis and Quebec's Dairy Farms, Canadian Journal of Agricultural Economics, 41, 169-176.

Coelli, T.J. (1996), A Guide to DEAP Version 2.1: A Data Envelopment Analysis (Computer) Program, CEPA Working Paper 96/08, Centre for Efficiency and Productivity Analysis, University of New England.

Coelli, T.J., Rao, P.D.S. and Battese, G. (1998), An Introduction to Efficiency and Productivity Analysis,  Kluwer Academic Publishers: Massachusetts.

Doucouliagos, H. and Hone, P. (2000), Deregulation and Subequilibrium in the Australian Dairy Processing Industry, The Economic Record, 76, 152-162.

Edwards, G. (2003), The Story of Deregulation in the Dairy Industry, Australian Journal of Agricultural and Resource Economics, 47, 1-24.

Farrell, M.J. (1957), The Measurement of Productive Efficiency, Journal of the Royal Statistical Society, A CXX, 253-290.

Fraser, I.M. and Cordina, D. (1999), An Application of Data Envelope Analysis to Irrigated Dairy Farms in Northern Victoria, Australia, Agricultural Systems, 59, 267-282.

Jaforullah, M. and Whiteman, J. (1999), Scale Efficiency in the New Zealand Dairy Industry:  a Non-parametric Approach, The Australian Journal of Agricultural and Resource Economics, 43, 523-541.

Kumbhakar, S.C., Ghosh, S. and McGuckin, J.T. (1991), A Generalized Production Frontier Approach for Estimating Determinants in US Dairy Farms, Journal of Business and Economic Statistics, 9, 279-286.

Simar, L. and Wilson, P.W. (2000), Statistical Inference in Nonparametric Frontier Models: The State of the Art, Journal of Productivity Analysis, 13, 49-78.

Sincich, T. (1996), Business Statistics by Example, Prentice Hall: New Jersey

Tauer, L. and Siefanades, Z. (1998), Success in Maximising Profits and Reasons for Profit Deviation on Dairy Farms. Applied Economics, 30, 151-156.

Weersink, A., Turvey, C.G. and Godah, A. (1990), Decomposition Measures of Technical Efficiency for Ontario Dairy Farms, Canadian Journal of Agricultural Economics, 38, 439-456.

Zhang, Y. and Bartels, R. (1998), The Effect of Sample Size on the Mean Efficiency in DEA with an Application to Electricity Distribution in Australia, Sweden and New Zealand, Journal of Productivity Analysis, 9, 187-204.