Australasian Agribusiness Review - Vol.18 - 2010
Paper 4
ISSN 1442-6951
Measuring Beef Cattle Efficiency in Australian Feedlots: Applying Technical Efficiency and Productivity Analysis Methods
Euan Fleming*, Pauline Fleming, Garry Griffith and David Johnston
Euan Fleming is a Professor in the School of Business, Economics and Public Policy at the University of New England; Pauline Fleming is a Lecturer in the School of Business, Economics and Public Policy at the University of New England; Garry Griffith is a Principal Research Scientist in the NSW Department of Primary Industries at Armidale and Adjunct Professor in the School of Business, Economics and Public Policy at the University of New England; and David Johnston is a Senior Scientist in the Animal Genetics and Breeding Unit, University of New England.
Contact information:
Euan Fleming, School of Business, Economics and Public Policy, University of New England, Armidale, NSW 2351, Australia.
Email: efleming@une.edu.au
Contact Euan Fleming for better quality graphs.
Abstract
Intensive livestock systems differ from most pasture-based systems in that managers exert much greater control over the production cycle and the quality of animals entering the system. Consequently, technical inefficiencies among animals tend to be much more easily eradicated. Nevertheless, a range of factors could still cause both technical inefficiency and variations in productivity between animals. These factors are the focus of analysis in this study of a beef cattle feedlot system operating under experimental conditions.
Technical efficiency and productivity analyses usually focus on the activities of firms or institutions using inputs to produce outputs, and the differences between them (Fleming et al. 2006). In this paper, we report on the efficiency with which physical characteristics of individual lot-fed beef cattle are combined with conventional inputs to produce a final product with several attributes. Data on 214 animals across seven breeds were used to estimate a stochastic input distance function with multiple inputs and multiple outputs. Estimates were obtained after controlling for differences between breeds, years and sex.
A high mean technical efficiency was estimated for the cattle as a group but it was found that different breeds have significantly different output frontiers and inefficiency levels. These differences are most likely associated with variation in genetic merit between sires within and between breeds and the different farming and climatic backgrounds of the animals' cohorts.
Results are reported on the input-output relationships as well as the relationships between the outputs. Important findings in respect of output relationships in this sample are that the proportion of meat weight retained after cooking is positively associated with the meat quality sensory score, and carcass weight is negatively associated with the meat quality sensory score. No relationship was discerned between carcass weight and the proportion of meat weight retained after cooking.
It is expected that the further application of these technical efficiency and productivity analysis methods to physical cattle data will lead to improvements in the valuation of different animal attributes in genetic selection software packages.
Keywords: intensive beef, input distance function, diversification economies, technical efficiency.
1. Introduction
Intensive livestock systems differ from most pasture-based systems in that managers exert much greater control over the production cycle and the quality of animals entering the system. Consequently, technical inefficiencies among animals tend to be much more easily eradicated. This is especially so when the intensive livestock system in question operates under experimental conditions. Nevertheless, a range of factors could still cause both technical inefficiency and variations in productivity between animals and across breeds:
- variations in the genetic potential of sires and dams;
- variations in environmental conditions prior to animals entering the backgrounding phase of the production cycle (the phase when feedlot managers take control of the animals);
- catch-up effects when genetic advances between breeds take place at different rates;
- inherent differences in the productive potential of breeds in feedlotting, especially between temperate and tropically adapted breeds where it is expected that the former would be more productive than the latter; and
- different rates of genetic advances between breeds.
In this paper, we test the proposition that no technical inefficiency is present in the feedlot system under study. If technical inefficiency is found to exist, we then test the proposition that it does not differ between breeds. We also test the proposition that no variations in productivity exist between breeds, either within temperate or tropically adapted breeds or between temperate and tropically adapted breeds.
Most analyses of technical efficiency and productivity focus on the activities of firms or institutions using inputs to produce outputs, and the differences between them. For example, in a recent paper in this Review, Fleming et al. (2006) proposed the more widespread application of modern technical efficiency and productivity analysis methods to issues of benchmarking complex Australian farm businesses and of comparing their economic outcomes. A number of case studies were reported where the methods were applied and new information was able to be generated. There is a growing international literature where such methods are being applied to farm business performance comparisons (see for example, Newman and Matthews 2007).
The analysis reported here differs from this conventional approach in that we focus on individual animals rather than firms as production units. The analysis is set in the context of how efficiently individual lot-fed beef cattle can be turned into meat output with multiple attributes. We specify and estimate production relations from the time cattle enter a feedlot to the stage where meat is produced. A stochastic input distance function is used to allow production relations to be expressed in terms of best performance rather than average performance. The frontier in meat production performance is of particular interest. Technical efficiency indices are calculated to assess each animal that passes through the feedlot, to indicate the extent to which its performance deviates from the frontier. The estimated technical efficiency indices are compared with conventional estimates of feed-use efficiency. Another focus of our analysis is on the relations between the characteristics of meat output, reflecting their complementarities and trade-offs. To this end, we use results from the estimated stochastic input distance function to measure diversification economies in feedlot beef production.
It is anticipated that the further application of these technical efficiency and productivity analysis methods to physical cattle data could lead to improvements in the valuation of different animal attributes in genetic selection software packages. For example, BreedObject (Barwick and Henzell 1997, 1998) is a tool for formalising beef cattle breeding objectives through the use of $Indexes. For a given bull, it draws together the BREEDPLAN estimated breeding value (EBV) figures on different traits and the estimated marginal economic return from more of the trait into a single EBV, the $Index, which describes how well that bull suits a particular purpose. While genetic interactions are accounted for, no account is taken of inputs other than genetics in defining the $Index. Our expectation is that future developments in technical efficiency and productivity analysis methods will lead to improvements in how packages like BreedObject are specified and applied.
2. Variables and data
The data used in the analysis are a sub-set of the data described and analysed extensively by Johnston et al. (2003a), Reverter et al. (2003a), Johnston et al. (2003b) and Reverter et al. (2003b). They were collected as part of a straight-breeding project implemented by the Cooperative Research Centre for Cattle and Beef Quality (Beef CRC). The aim of the project was to estimate genetic and phenotypic relationships between measures of animal, carcass and meat quality characteristics (Burrow et al. 2003).
The sub-set of data we use consists of 214 cattle across four temperate breeds (Hereford, Angus, Shorthorn and Murray Grey) and three tropically adapted breeds (Belmont Red, Brahman and Santa Gertrudis). The breeds are randomly allocated a relevant code for analysis as Temp1, Temp2, Temp3, Temp4, Trop1, Trop2, or Trop3. The meat from these cattle is produced to the Korean market standards (around 280 kg carcass weight), after approximately 100 days in the feedlot. Details on cattle included in the sample for estimating the model are presented in Table 1. Only the Trop2 and Trop3 breeds contain heifers; all other breeds consist solely of steers. Also shown are numbers of breed cohorts entering feedlots across years and seasons in the sample.
Table 1. Information on the Sample
Breed |
Temp1 |
Temp2 |
Temp3 |
Temp4 |
Trop1 |
Trop2 |
Trop3 |
Heifers |
0 |
0 |
0 |
0 |
0 |
35 |
15 |
Steers |
53 |
36 |
19 |
11 |
16 |
18 |
11 |
Total |
53 |
36 |
19 |
11 |
16 |
53 |
26 |
Entry liveweight |
398 kg |
398 kg |
336 kg |
415 kg |
397 kg |
373 kg |
415 kg |
Cohorts |
9 |
6 |
3 |
2 |
3 |
3 |
4 |
Years |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
Seasons |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
Johnston et al. (2003a) described the data collected on 20 animal, carcass and meat quality traits and the measurement procedures they used. Many of these traits are included in this study. Six animal traits, measured on entry to the feedlot, are included as inputs in the production process: age (in days), liveweight (in kilograms), rib fat depth (in millimetres), rump fat depth at the P8 site (in millimetres), eye muscle area (in square centimetres) and muscle score.
We also included two conventional inputs, namely individual feed intake per day (measured using automatic feeders) and number of days in the feedlot. The latter variable is included to capture inputs common to all animals (veterinary supplies, supervision, provision of feeding facilities and other capital structures) as well as the number of days of feed intake. The fact that no data are available on the amounts of those inputs common to all animals is not considered a drawback. It is reasonable to assume that they are the same for each animal and can be measured by the amount of time that an animal spends in the feedlot.
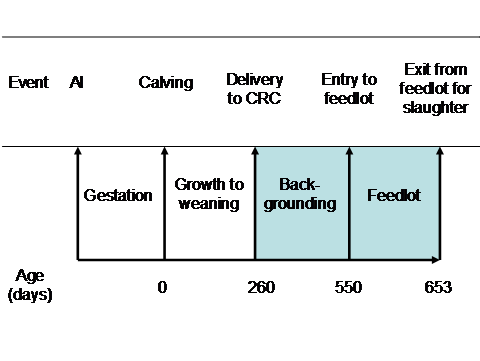
Slaughtering and post-slaughter inputs are omitted from this study. However, Johnston et al. (2003b, p. 136) reported that considerable effort was made to standardise these inputs. Also, animals were subject to similar backgrounding prior to entry to the feedlot. All animals were received by the Beef CRC as weaners prior to backgrounding. Variations occur in physical characteristics among animals of the same breed entering the backgrounding stage due to herd-of-origin effects brought about by differences between cohorts in sires and dams, and seasonal conditions in the pre-weaning stage. Figure 1 gives the timetable for preparing cattle to Korean market standards. The shaded area shows the period during which the cattle were under the control of the Beef CRC management.
Figure 1. Timetable for preparing lot-fed cattle to the Korean market standards
Four output variables are included in the analysis: amount of carcass weight produced, proportion of carcass weight retained after cooking, meat quality and marbling. The amount of carcass weight produced is measured as hot carcass weight in kilograms. The proportion of carcass weight retained after cooking was derived from a variable reported by Reverter et al. (2003b, p. 151) as cooking loss percentage. Because it is desirable for output variables in a production function to have positive relations with inputs, retention weight after cooking was calculated as a percentage by subtracting cooking loss percentage from 100.
A composite index of four sensory measures of quality was used to measure the quality of meat output. Johnston et al. (2003b, p. 137) termed this variable the sensory MQ4 score, including tenderness, juiciness, flavour and overall acceptability scores[1]. Because of the very high correlations among all of these four individual scores (Johnston et al., 2003b, p. 143), we expect to lose little information by using the composite index rather than four individual meat quality variables.
Two alternatives were available to represent the marbling of meat: the proportion of intramuscular fat and a discrete marbling score specified by AUS-MEAT (1998). The former was preferred because it is a continuous variable.
3. Model specification
We use a multi-input multi-output stochastic input distance function (Coelli and Perelman 1996, Coelli and Fleming 2005) to calculate technical efficiency indices for each sampled lot-fed animal, mean technical efficiency for each breed and mean technical efficiency across all animals. A stochastic input distance function is used rather than the standard stochastic production function to accommodate the specification of more than a single output. The eight inputs in the model are feed intake, number of days in the feedlot, age, liveweight, muscle score, rib fat depth, rump fat depth and eye muscle area. The four outputs are carcass weight, meat quality, retention of weight and marbling.
Zero-one dummy variables are included in the distance function for year, heifer and breed. As the data observations spanned 1996 and 1997, a 1997 dummy variable is also included to test for any difference in productivity between years. The details of this model are provided in Appendix A for interested readers.
4. Estimates of production relations
4.1 Input-output relations
Estimates of input and output elasticities from the maximum-likelihood estimation of the stochastic input distance function model and their standard errors are presented in Table 2. We are particularly interested in the output elasticities, which are the coefficients of the input variables in the estimated model. They measure the percentage increase in all outputs for a one per cent increase in the use of each of the inputs. The sum of the estimated elasticities of the input variables is 0.78, so given the restriction required for homogeneity of degree +1 in inputs, the implied output elasticity for the omitted variable, age of the animal when entering the feedlot, is 0.22. Individual likelihood ratio tests on each input and output showed that all but one input and one output contribute significantly in model estimation.[2]
Table 2. Estimates of the Input and Output Elasticities
Variable |
Estimated elasticity |
Standard error |
t-value |
Inputs: |
|||
Feed per day |
0.10 |
0.010 |
9.99 |
Days in feedlot |
0.53 |
0.0092 |
57.62 |
Liveweight |
0.10 |
0.021 |
4.90 |
Rib fat depth |
0.0080 |
0.0035 |
2.26 |
Rump fat depth |
-0.0024 |
0.0039 |
-0.61 |
Eye muscle area |
0.015 |
0.011 |
1.36 |
Muscle score |
0.022 |
0.010 |
2.28 |
Outputs: |
|||
Carcass weight |
-0.237 |
0.014 |
-16.56 |
Weight retention |
-0.252 |
0.040 |
-6.26 |
Meat quality |
0.014 |
0.006 |
2.20 |
The number of days in the feedlot is highly significant and has the highest elasticity at 0.53. Other elasticities estimated to be significantly greater than zero are daily feed intake and weight on entering the feedlot (each 0.10), muscle score (0.02), eye muscle area (0.015) and rib fat depth (0.01). Only the estimated coefficient for the rump fat depth variable is insignificantly different from zero. The elasticities of the animal characteristics are low, but these characteristics are virtually costless to maintain once they are established, in contrast to conventional inputs that need to be applied each year.
Coefficients on the two output variables, carcass weight (-0.237) and proportion of meat weight retained after cooking (-0.252), are negative, as expected, and highly significant at less than one per cent significance level. They reflect a positive impact of the set of input variables on these two outputs: a 10 per cent increase in all inputs would increase carcass weight by 2.4 per cent and the proportion of meat weight retained after cooking by 2.5 per cent. The significant and positive coefficient on the meat quality output variable was not expected. It indicates that the set of inputs as a whole have a negative impact on meat quality, although the small size of the estimated elasticity (0.014) suggests the magnitude of this impact is not very great. A possible explanation of this unexpected result is that the high correlation between meat weight retention and meat quality, and the highly significant impact of inputs on the former, is masking the true impact of inputs on meat quality. The marbling output variable (intramuscular fat percentage) was found not to be significantly influenced by the set of inputs[3]. A likelihood ratio test revealed that its omission from the estimated model had no significant effect and it is not reported in the results in Table 2.
4.2 Breed, heifer and year effects on productivity
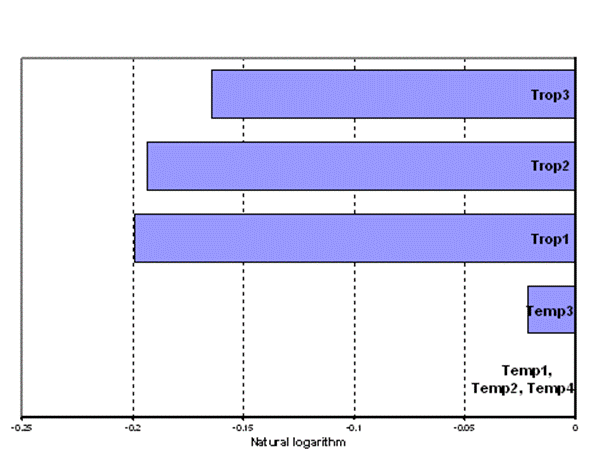
Individual likelihood ratio tests were conducted on the breed, year and heifer dummy variables in the distance function. In relation to breeds, Figure 2 shows the production frontiers of each breed of cattle in the sample. The frontiers of Temp1, Temp2 and Temp4 cattle are furthest from the origin (most productive). They are insignificantly different from each other, although it proved difficult to exactly place the frontier for Temp4 cattle given their small number of observations.
The frontier of Temp3 cattle is slightly but significantly below that for these three breeds (its scale parameter is 2.1 per cent less than that of the frontier breeds). The frontiers of the three tropically adapted breeds are much lower than the frontiers of the temperate breeds (scale parameters are lower than frontier breeds by 15.2 per cent for Trop3, 17.6 per cent for Trop2 and 18.1 per cent for Trop1).
A significant and positive coefficient for the 1997 year dummy variable indicates that feedlot productivity was higher in that year than in 1996. A significant and negative coefficient for the heifer dummy variable indicates that tropical heifer productivity is lower than steer productivity. The effect of this dummy variable is to reduce the scale parameter for heifers to around 2 per cent less than the parameter for steers.
Figure 2. Comparison of production frontiers by breed
Frontier differences
5. Technical inefficiency estimates
5.1 Evidence of technical inefficiency
The value of the test statistic for the null hypothesis of no technical inefficiencies of production (96.65) was found to be greater than the critical value obtained from Table 1 of Kodde and Palm (1986) for eight restrictions (14.85). We thus conclude that the technical inefficiency term (ui in equation 1) is a significant addition to the model. A likelihood-ratio test that the coefficients on the breed efficiency variables are zero is strongly rejected, indicating that these variables as a group contribute significantly to an explanation of technical inefficiency in lot-fed beef production.
The gamma value (in equation 1), reflecting the percentage of error due to inefficiency, is not significantly different from unity, indicating that all residual variation is attributable to inefficiency and the random error is negligible. The lack of random effects reflects the strong control that managers have over the production environment in feedlot operations.
5.2 Influence of breed on technical inefficiency
The distance that cattle are located away from the frontier is likely to be influenced by variations in production potential among progeny from different sires and recent advances in breeding technology. It is proposed that performance is more tightly grouped (the mean technical efficiency index is higher) among breeds where the progeny come from a small pool of sires and the breed has not experienced substantial genetic advances in recent years.
These propositions are tested by including six breed dummy variables in the inefficiency effects model. The seventh breed, which is Temp1, is treated as the base. Given that Temp1 progeny come from the widest pool of sires that have experienced considerable recent genetic advances, it is expected that the signs on the coefficients of the six breed dummy variables will be negative, indicating lower technical inefficiency than Temp1.
All z-variables included in Table 3 except two contribute significantly (jointly and individually) to the explanation of technical inefficiencies in feedlot beef production. The Temp4 and Trop3 dummy variables are the exceptions (with both failing at the 5 per cent significance level).
Table 3. Estimates of the Efficiency Model
Variable |
Estimated coefficient |
Standard error |
t-value |
Constant |
0.041 |
0.0046 |
8.81 |
Temp2 dummy variable |
-0.017 |
0.0087 |
-1.93 |
Temp3 dummy variable |
-0.048 |
0.0140 |
-3.41 |
Temp4 dummy variable |
0.0084 |
0.0047 |
1.80 |
Trop1 dummy variable |
-0.21 |
0.0217 |
-9.47 |
Trop2 dummy variable |
-0.063 |
0.0161 |
-3.94 |
Trop3 dummy variable |
-0.010 |
0.0080 |
-1.26 |
Sigma squared |
0.00042 |
0.00002 |
24.99 |
Gamma |
0.999 |
0.011 |
90.82 |
Plots of the distribution of the technical efficiency indices by breed are presented in Figure 3, with indices varying from 0.92 to 1.00. This is a narrow range but one to be expected given the controlled environment and identical management the animals receive from weaning through to slaughter. The high mean technical efficiency index indicates that a small but significant opportunity exists to increase beef output without using more physical and genetic inputs.
Figure 3. Distribution of technical efficiencies by breed
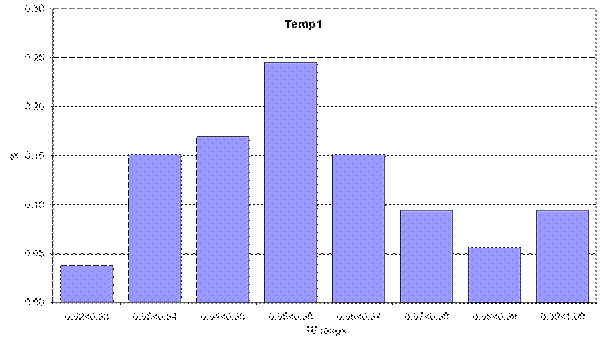
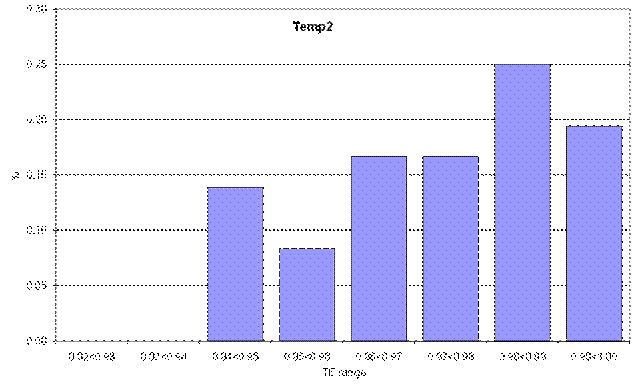
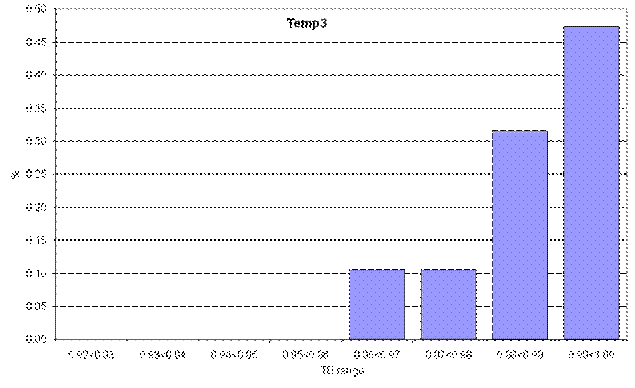
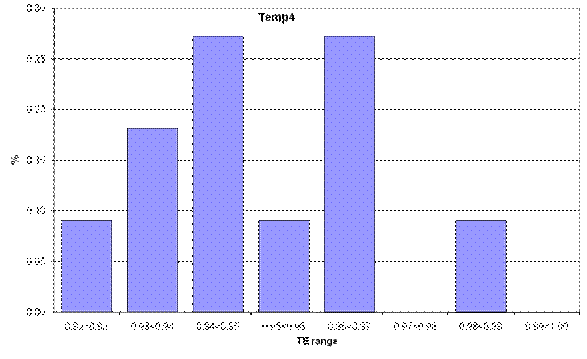
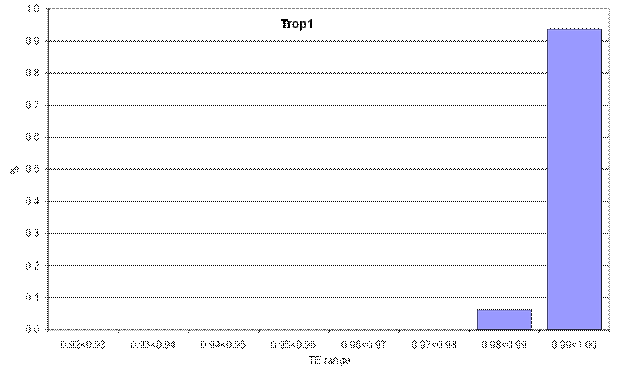
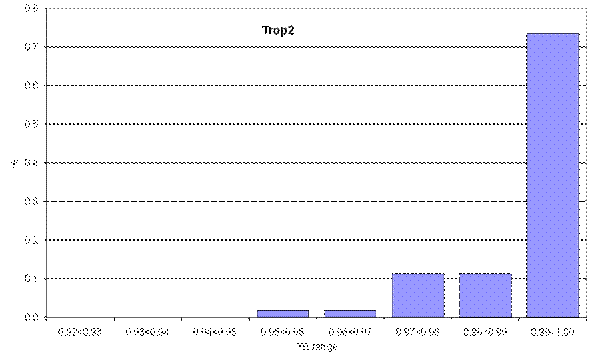
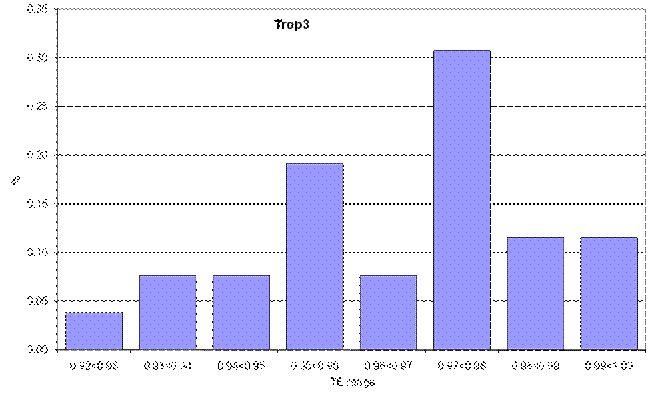
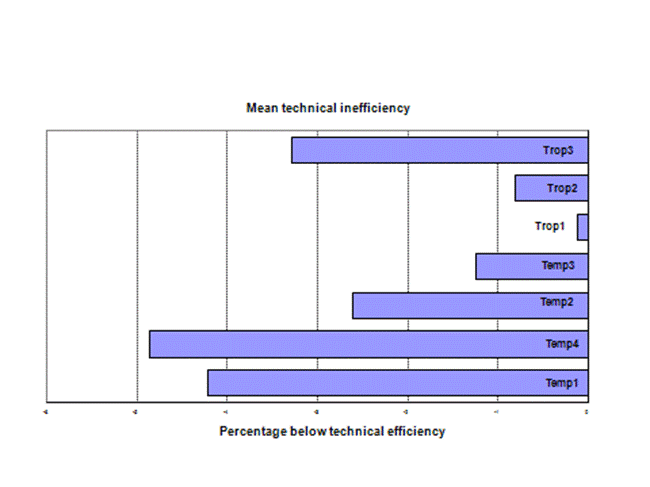
Controlling the quality of sires of progeny entering the feedlot is a way to raise technical efficiency. This point is illustrated in Figure 4. The mean technical efficiencies of each breed are to be interpreted relative to the frontier. Figure 4 shows the percentage by which the mean technical efficiency of each breed is less than perfect technical efficiency (100 per cent) (that is, below its frontier.
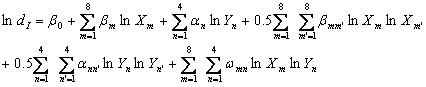 (1)
(1)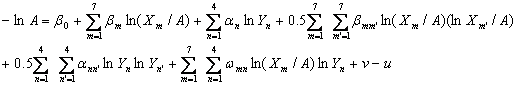 (2)
(2)