Depreciation Rates for Australian Tractors and Headers - Is Machinery Depreciation a Fixed or Variable Cost?
Peter R. Tozer
Research Economist at the Department of Agriculture Western Australia, Geraldton, Western Australia.
Email: ptozer@agric.wa.gov.au
Abstract
Seven different remaining value functions for tractors and harvesters were estimated using data from advertised prices for used farm equipment. The generalised Box-Cox model was used to nest six of the seven functions. The more complex Box-Cox function explained the data no better than simpler models such as the linear, sum-of-the-year’s-digits, or double-square root models. The simpler functions were easier to manipulate to estimate depreciation rates and costs. There were up to four components of depreciation, drive-away, brand, age, and use related, depending on functional form. Drive-away depreciation is the immediate loss in value of a machine due to purchase, in some models this depreciation cost was higher than either age or use related depreciation costs. When drive-away depreciation was treated as a separate cost to age and use depreciation, or when there was no drive-away depreciation due to functional form, the age to use depreciation cost ratios were in the range of 1.5-2 to 1. Hence, tractor and header depreciation is a combination of fixed and variable depreciation.
Introduction
Depreciation is the cost associated with capital equipment ownership to account for use, obsolescence, and, supposedly, as a means to save for the replacement of capital items. Typically, it is assumed that depreciation is a fixed cost. The rationale for this assumption is that the major component of depreciation is based on the age of the capital item and that use does not significantly affect the value of the item (Heady and Jensen 1954; James and Eberle 2000). However, it would be reasonable to assume that there are at least two factors that cause depreciation, age and use (Perry et al. 1990). The value of a machine can decline simply by sitting unused because of obsolescence of the technology embedded in the machine. Use causes depreciation, even in new machinery because of wear and tear on the components within the machine which could shorten the usable life of the machine. Therefore, it would be rational to decompose the depreciation cost into two cost elements, fixed, which would be age-related, and variable, which is use-related, when developing enterprise and whole farm budgets. With the variable component assigned pro-rata to the enterprises utilizing the machine and the fixed factor deducted from operating profit. Many extension publications assume that the depreciation cost is a linear function of the initial purchase price, salvage value and expected life of the piece of machinery (Anon 2004; Harris 2002). However, this method requires assumptions being made concerning the expected life of the equipment and the salvage value (Makeham and Malcolm 1993).
The costs of owning and operating machinery can account for the majority input costs for a broadacre copping enterprise (Kruger and Logan 1980; Wu and Perry 2004). These operating and ownership costs include fuel, oil, repairs and maintenance, insurance, and depreciation. Depreciation can impact the relative profitability of production decisions (Reid and Bradford 1987) through differential use in various crops because of varying work speeds caused by for example, crop density, crop type, harvesting constraints, and or soil type.
The majority of studies regarding machinery depreciation have utilized data from North America; no machinery depreciation studies have been undertaken using Australian data, the exception being the study of Kruger and Logan (1980), which was based on a set of 33 observations and in this case only the exponential functional form was tested. Also, none of these studies have explicitly answered the question: how do factors other than age affect the annual machinery depreciation costs for agricultural producers? These studies have provided parameter estimates, but have not shown how these models and parameters affect the fixed and variable costs of depreciation to the producer. The objective of this paper is to estimate remaining value functions for tractors and combine harvesters using data from Australia, to test a set of functional forms to determine which, if any, are better suited to the estimation of the fixed and or variable costs components for extension and research purposes, and to determine if depreciation is a fixed or variable cost or a combination of both.
Empirical Model
The remaining value (RV) function is an equation that allows researchers and extension workers to estimate the residual value of a piece of capital equipment using knowledge of initial cost, age, usage and other variables that may impact on value. These variables can include size, condition, power, manufacturer, and location of sale of machinery. One benefit of the RV function is that it is not necessary to make assumptions regarding the salvage value of the equipment (Dumler et al., 2000; Perry et al. 1990; Wu and Perry 2004). Machinery RV, which is calculated as the current value of the capital item as a percentage of the initial real purchase cost, can be represented in general form as:
RV = ¦ (age, usage, manufacturer, power, drive, size, condition, other factors) (1)
The range of functions used to calculate RV is varied. The American Society of Agricultural Engineers (ASAE) (in Siemens and Bowers 1999) suggests that the remaining value of farm machinery can be estimated using an exponential function as follows:
RV = a(b)Age (2)
Where, in the ASAE standards, a = 0.68 and b = 0.94 for tractors and headers (Siemens and Bowers 1999). This equation has been shown to be a poor estimator of remaining value due to the inflexibility inherent in the function caused by the fixed parameters (Wu and Perry 2004). Kruger and Logan (1980) concluded that the parameter values of the ASAE model for American machinery were not applicable to Australian tractors and that different values were estimated for Australian machinery.
Weersink and Stauber (1988) used a log-linear functional form to estimate the remaining value function for grain combines in Canada. This function fitted the data well, but there was no inclusion of other variables in the functions such as usage to determine if these variables affected the remaining value. Other researchers have used linear, Cobb-Douglas, or exponential functions to estimate remaining value (Wu and Perry 2004). Each of the forms mentioned imposes restrictions on the ability of the data to explain depreciation rates over time. Hence, Perry et al. (1990) suggested the use of the Box-Cox flexible functional form as a means of more accurately capturing the effects of different variables on depreciation rates and patterns. The general Box-Cox RV function is written as:
![]() (3)
(3)
Where RV is the remaining value, xi and Zj are two subsets of independent variables, one transformed and the other not. The transformation variables l and gi are for the dependent and independent variables, respectively. Solving equation 3 for RV yields:
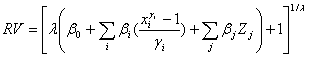 (4)
(4)
The value of the transformation variables can determine the type of depreciation function: when l = 1 and gi = 1 depreciation is linear; when l = 0.5 and gi = 1 the function replicates the sum-of-the-year’s digits (SYD) form; l = 0 and gi = 0 indicates that depreciation takes the Cobb-Douglas form; when l = 1 and gi = 0.5 the square root function is assumed, and for l = 0.5 and gi = 0.5 the function is a double square root. When l and gi are estimated they have the following general properties, if l < 0 and gi £ 1 then depreciation rates are declining over time, if the opposite holds then depreciation rates are increasing over time (Wu and Perry 2004). In the case when l = 0 or gi = 0 the function is estimated using the natural logarithm of RV or xi.
The RV function provides an estimation of the value of a capital item, but can also be utilized to estimate the depreciation rate and annual costs. Depreciation rate (RATE) in the general Box-Cox model is equal to (Wu and Perry 2004):
![]() (5)
(5)
where, if we assume that the depreciation rate relates to one of the transformed variables;
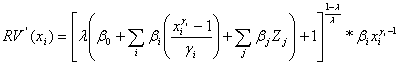 (6)
(6)
and;
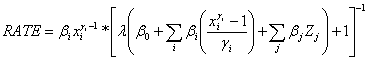 (7)
(7)
By using this equation it is possible to
calculate annual depreciation costs for any transformed variable of interest.
It is also possible to calculate the depreciation rate for non-transformed
variables through manipulation of equation 4. This yields an equation similar
to equation 7 except the numerator is ![]() rather than
rather than![]() .
.
Depreciation Costs Case Study
A case study will be used to demonstrate the application of the results of the empirical models. Estimating annual depreciation costs using the remaining value functions derived is possible using several easily accessible pieces of information: the new price of the piece of machinery, expected usage and age. In this study we use a simple case study to demonstrate the calculations and effects of different functional forms on annual depreciation costs. The case study will use a new harvester with a price of $322 000 and brand is fixed at the mean value for the brand variable of 1.5652. It is assumed the harvester will be used for four years then traded for a newer model and annual usage is 400 hours per year. Using a textbook straight-line depreciation method over four years with a trade-in or salvage value of 50 per cent of new value of $161 000, the estimated the annual depreciation cost is calculated to be $40 250 per year. In this paper only a header example is shown, however, it is possible to follow similar logic for calculating tractor depreciation using the parameters estimated.
Data
The data for the models estimated in this study are based on machinery dealer advertised prices for tractors and headers less GST if GST was included in the advertised price as GST is not included in the manufacturer’s new list price. The data were obtained from a search of internet sites of agricultural machinery dealers across Australia over the months of September to December 2004 and are summarised in Table 1. In previous studies actual sales price was used; however in this study actual sales prices were not available. The advertised prices include dealer mark-ups to cover warranty costs and repair expenses that could be or were incurred to get the machine to sale quality. Tests on the data show that reducing the advertised price by various percentages to capture mark-ups changed the remaining value by approximately the same percentage, indicating that the functions were changing the intercept value but not the slopes. Hence, the depreciation rates and costs are not affected by dealer mark-ups only the remaining value of the machine, this is consistent with the comments of Unterschultz and Mumey (1996).
Each observation for the harvester data set contained information on manufacturer, year of manufacture, total hours of use, front width, and price. Tractor data contained information on manufacturer, year of manufacture, total hours of use, engine power, type of drive (four-wheel, front wheel assist, or two wheel), and price. Tractors with attached equipment, such as front-end loaders or fork lifts were excluded from the data set. Data on other variables such as condition were not included as the data either included photographs from which it was difficult to discern condition or the dealer did not list the condition. Because of the need for a complete observation to contain the minimum information listed above, the number of potential data points was limited, as many advertisers did not include at least one piece of critical information, hence the small size of the data set.
Total hours of use was converted to average hours of use per year (HPY) to reduce the possibility of multicollinearity affecting the estimates due to relatively high correlation between the age and total hours variables. The correlation coefficient for the age and total hours variables was 0.7784 and 0.5448 for the harvester and tractor data, respectively. Correlation coefficients for age and HPY were -0.1524 (harvesters) and -0.3650 (tractors) indicating low to moderate correlation between the two variables.
The harvester data includes machines manufactured from 1990 through to 2003. Data were available on a small number of harvesters manufactured prior to this period, however because of the sparse nature of this data it was deemed unsuitable for the study. Tractor data covered the period 1989 through 2003. Again data were available for a small number of machines manufactured prior to 1989 but were not utilized for the same reason as for harvesters.
The harvester data set of 115 observations was dominated by two manufacturers, John Deere and Case. These two manufacturers accounted for 76 per cent of the harvester observations. Machines from three other manufacturers, New Holland, Allis-AGCO, and Massey Ferguson, completed the data set. List prices for the harvesters included in the data were obtained from the Power Farming Harvest Annual (Power Farming various dates). The tractor data set of 68 observations was again dominated by the same two manufacturers as before, in this particular set representing 71 per cent of observations. The remaining data represented six other manufacturers, Ford, New Holland, AGCO, JCB, Fiat and Caterpillar. For both tractor and harvester sets some of these manufacturers have, over the period covered, merged: hence, some brands may not now exist or are manufactured by one company rather than two or more, i.e. Ford, Case and New Holland. Each manufacturer was assigned a dummy variable from zero to three, where one and two represent the two largest manufacturers, respectively, three for New Holland, and zero capturing all other minor manufacturers.
List prices for tractors were obtained from the fourth edition of Power Farming every year from 1989 until 2004 to maintain consistency of recording time. Unterschultz and Mumey (1996) suggest that the manufacturer’s list price not be used in an analysis of depreciation as the list price may be higher than actual market price for new machines due to marketing methods used by manufacturers. However, to accurately estimate depreciation a new price is needed and, as list price is available and easily accessible, these are used in this study. Other published studies, such as Perry et al. (1990) and Cross and Perry (1995) have utilized similar information. List prices were converted to real 2004 prices by weighting the list prices by the index of plant and machinery costs reported in ABARE (2003; 2004). The price index was adjusted such that 2004 was the base year, so that real list and current sales prices were in the same real values. Wu and Perry (2004) also included indices of farm income and interest rates in a multiyear study of machinery depreciation: however, as this current study covers one-year’s data these variables were not necessary.
Results and Discussion
Models
The general Box-Cox model was used as a basis for the harvester and tractor models estimated and the form of the Box-Cox model for this study was:
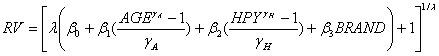 (8)
(8)
The models that can be derived from the Box-Cox functional form that were used in this study are: linear; Cobb-Douglas (C-D); sum-of-the-year’s digits (SYD); square root (SQR); double square root (DSQR); and the Box-Cox transformation (BCT). The exponential function model, as described by the ASAE was also modelled, however, in this study a and b were estimated rather than utilize the fixed parameters specified earlier. The ASAE model was included in the study to compare its performance against the other functional forms. All models were estimated using the PROC MODEL procedure in SAS (SAS 1999). Model comparison is based on goodness-of-fit statistics including adjusted R2 and log of the likelihood function.
Preliminary Models
Several preliminary models were tested using different sets of variables to determine which initial combination of variables best explained RV. The basic model for the harvester data included age, brand, and average hours of usage per year. Other models were tested; these included regressing RV on age, total hours, or hours per year individually. All these models yielded unsuitable results based on tests for heteroscedasticity or goodness-of-fit. Some of these results were expected, particularly with respect to the model of RV on age which is the typical model used in estimating depreciation. This model did not fit either set of data as well as the models that included hours per year, brand and age. A model of RV and total hours was an inferior fit to the models including age and hours per year. These models also exhibited high levels of heteroscedasticity using White’s test (P < 0.0001).
Wu and Perry (2004) estimated models for tractors of 5 different horsepower levels, however given the small data set used in this study this was not possible. Also, preliminary testing on models including engine horsepower showed that horsepower was not a variable that significantly affected the remaining value of tractors.
Models of RV Function
The results derived from the general Box-Cox model for the harvester models, as shown in Table 2, suggest that the linear, SYD, SQR, DSQR, and BCT functions explain the depreciation data better than the C-D or the ASAE forms based on the log likelihood functions. There were no differences between the linear, SYD, SQR, DSQR and BCT models in terms of likelihood ratio tests, which contrasts with the results of Wu and Perry (2004) who found that the Box-Cox models were statistically superior to all other functional forms in estimating depreciation of harvesters.
The set of functions that fitted the tractor data best were the BCT, DSQR and SQR models, with no statistical difference between these three functions, which again is counter to the results of Wu and Perry (2004). The linear, C-D and SYD models were comparable to each other in terms of likelihood ratio tests, but were poorer fits than the BCT, DSQR and SQR functions.
The ASAE model fitted the harvester data relatively poorly with goodness-of-fit statistics, measured by the adjusted R2 and log-likelihood function, well outside comparable ranges of the other models, only the C-D model fitted worse. In the case of the tractor models the ASAE model fitted the data worst with the lowest adjusted R2 and the lowest log-likelihood, indicating a poor fit. As the ASAE model can be nested in the general Box-Cox, the model can also be compared to the others using the likelihood ratio test as the model. Likelihood ratio tests show that the ASAE model is significantly different to the linear, SYD, SQR, DSQR, and BCT functions as well as the C-D function for the harvester data, and different to all functions in the tractor models. The C-D function had the poorest fit of all the harvester models, based on adjusted R2 and log likelihood, and was significantly different from all models including the linear model.
Although the BCT function fitted well in both sets of models, based on the likelihood ratio statistic and the adjusted R2, the fit of individual parameters in the BCT models was relatively poor. In the harvester model three parameters were statistically greater than zero based on the approximate t-values calculated by SAS, one at 95 per cent (b2) and two at 90 per cent (b2, l). For the tractor model, three parameters, b2, b3, and gH, were statistically different from zero at 95 per cent for the first two and 90 per cent for gH.
Another problem that arose in the SQR, DSQR and BCT functions for both machine types was that the intercept for each of these functional forms was greater than one, implying that for the machine type studied it would be worth more used than it is new in the year of purchase. Intercepts greater than one imply that the machinery appreciates after sale and this can lead to an underestimation of annual depreciation costs. The intercept terms for the linear, ASAE and SYD function are all less than one, which would be expected, as new machinery loses value as soon as it is sold (Perry et al. 1990), and implies that there is a fixed component of depreciation that is not affected by any variable except the sale of the piece of machinery as described in Akerlof (1970).
The brand coefficient in the harvester and tractor models was positive and significant. This indicates that some brands have lower depreciation costs or rates compared to others; this will be discussed further in a subsequent section.
Depreciation rates
Utilizing equation seven to estimate the depreciation rate for each functional form’s transformed variables yielded a range of depreciation rates. The annual average age related depreciation rate for harvesters varied from 5.17 per cent to 12.36 per cent, and average usage depreciation rate per hour ranged from 0.03 per cent to 0.09 per cent. Depreciation rates for tractors followed similar ranges with age depreciation from 4.03 per cent to 12.23 per cent and usage from 0.02 per cent to 0.09 per cent. The average depreciation rates across machines types and functional forms were consistent, meaning that similar rates are estimated for the different machine types using the same functional form.
In this study only average annual depreciation rates are reported. However, most depreciation rates are not constant across age or usage rates. Wu and Perry (2004) showed that the linear and the SYD forms have increasing depreciation rates over time. This is not intuitively obvious, particularly for the linear function as the linear function has constant depreciation cost. The reason for the increasing depreciation rate is that the constant, bi is divided by a declining remaining value, therefore the depreciation rate increases over time. This effect can be observed more clearly in equation 6, the numerator is constant at bi as xg-1 = 1, and the denominator is declining as age or usage increases. For all other functional forms reported in this study the age depreciation rates are declining over time as expected. Usage depreciation rates followed similar patterns to the age functions.
Brand Effects on Depreciation Costs.
The effects of individual brand on remaining values and depreciation costs are presented in Table 4. The intercept terms for each group varies from 0.7539 to 1.0712, the age related parameter ranged from -0.0281 to -0.0636, and the use parameter took values from -0.0002 to -0.0009. Using the same information and costs for a harvester as in the previous example, the average annual depreciation costs varied from $32 314 to $47 568. The “others” brand group had higher annual depreciation costs and a lower log-likelihood function which may be due to the small sample size for this brand group. The John Deere brand had lowest annual depreciation costs, due to lower use-related depreciation. New Holland and the “others” brand groups had substantially higher use-caused depreciation costs and New Holland had considerably higher age-related costs. The two higher costs incurred by the New Holland brand harvesters were offset somewhat by a positive drive away depreciation cost. The major point that arises from the analysis of remaining values for individual brands is that the ratio of fixed to variable costs varies greatly. For the two major brands the ratio of fixed to variable costs are approximately 3.5:1, but for the other two groups the ratios are 0.37:1 and 0.51:1, indicating that use caused depreciation, and hence the hourly depreciation rate, in these brands is substantially higher than for the two major brands. This could have implications when determining which harvester brand to select for a particular enterprise or business, as the machinery costs could overwhelm the gross income and generate negative gross margins in some enterprises or years.
Depreciation costs case study
Beginning with the linear model; the estimated remaining value of the harvester after four years is $180 899, implying that the total depreciation over the period is $141 101. This depreciation cost is made up of four components; the fixed component due to sale (what will be termed here the drive-away depreciation), the age factor, usage element, and brand effect. The drive-away depreciation is $44 729 and the brand effect on depreciation cost is $20 457. These costs are incurred in the first year of ownership in addition to the annual age and use depreciation costs in that initial year. The age depreciation cost over the four years is $45 325, and total usage depreciation costs are $30 590. Averaging the four components together yields an annual depreciation cost of $35 275, which is less than the $40 250 estimated by the straight-line method. In this case the total fixed costs are $95 775 and the variable costs are $30 590, or $23 944 fixed and $7 648 variable costs per annum over the four years. These costs yield a ratio of fixed to variable costs of 3.13:1. Alternatively, the drive-away depreciation costs could be incurred in the first year, leaving the annual fixed cost at $11 331 and annual variable costs of $7 648. In the latter case the ratio is now reduced to 1.48:1.
The total depreciation costs over four years for the SYD and DSQR models are $162 540 and $163 411, respectively. Of the $162 540 depreciation in the SYD model, $76 349 is drive-away depreciation, including brand-related depreciation, incurred in year one, $52 890 is total age-related depreciation, and $33 301 is total use-caused depreciation, yielding $129 239 in fixed depreciation costs and $33 301 in variable costs, for an annual depreciation charge of $40 635, implying annual average costs of $32 310 fixed and $8 525 variable. The fixed to variable cost ratio is approximately 3.8:1. Again, this could be recalculated to incur the drive-away depreciation in year one, which gives average annual fixed depreciation of $13 222 and variable depreciation of $8 525, a fixed to variable ratio of 1.55:1.
For the DSQR model, given that the intercept is greater than one, any remaining value functions that yielded intercepts greater than the initial purchase were truncated to the purchase price otherwise they were left as calculated. As the DSQR model does not have an intercept less than one there is no drive-away depreciation, but there is a brand-related charge of $34 272 as well as age and use depreciation costs. These costs are $65 164 and $63 975, respectively. This yields a ratio of 1.55:1 of fixed to variable costs and these proportions remain relatively constant across all years. However, because of the nature of the DSQR function a large depreciation cost is incurred in the first year then depreciation costs decline over time. In this case the initial year depreciation cost, assuming a four year life, is 66 per cent of the total depreciation cost; the proportions of the depreciation cost in years two, three and four, are 14 per cent, 11 per cent, and 8 per cent, respectively. These proportions yield annual depreciation costs of $108 732, $23 629, $17 191, and $13 859 in years one, two, three and four, respectively, and an average annual cost of $40 853, with $24 849 age-related and $15 994 use-caused.
In general the average depreciation costs calculated in the textbook example are close to those estimated by the three different functions. However, the major differences between the textbook example and the three example functions are the timing of the costs and the types of costs incurred, whether they are age, use, brand or drive away depreciation costs. The textbook example, by implication, assumes there is no division of depreciation between fixed and variable costs; hence all costs are deducted from operating profit. The costs determined within each of the three example models can be assigned, pro rata to the gross margins or operating profit, depending on the type of cost. This allows a more accurate estimation of the costs of producing crops as variable depreciation costs are allocated to the crops causing the loss in value. There would be no difference in net operating profit after depreciation costs have been assigned as fixed or variable, as the total depreciation cost does not vary, only the allocation of these costs to either the individual crop gross margins or as a deduction from operating profit.
One problem that does manifest itself when attempting to calculate annual depreciation rates using the remaining value method and the models estimated, other than the linear function, is separating age and use related depreciation because of the functional forms and the interdependence of the two parameters. Although the more complex forms tended to fit the data slightly better, the simpler functions, i.e. linear or SYD, are more tractable to handle when estimating annual depreciation costs. As shown above the annual depreciation for the DSQR model is high in the first year, and then diminishes over time, whereas for the linear model the annual depreciation cost is constant over time, even though the depreciation rate is increasing.
Although, a high cost is also generated if the drive-away depreciation cost of the linear and SYD models is treated as a separate component. When drive-away depreciation is included as a separate component in the depreciation costs or in the case of the DSQR model, a high first year cost, the depreciation costs demonstrate a type of accelerated depreciation. The SYD model is already a type of accelerated depreciation function as depreciation costs are high in earlier years of ownership and decline over time. Neither the traditional straight-line method nor the DSQR are considered accelerated methods, but, in the case of the straight-line model with drive-away depreciation separate, and the high depreciation costs in year one of the DSQR model, it would be reasonable to allow that accelerated depreciation does occur in these models.
One objective of this research was to determine if depreciation was a fixed or variable cost or a combination. The research results suggest that depreciation is a combination of both. The ratio of fixed to variable deprecation varies from 3.18:1 to approximately 1.48:1. The major influence on this ratio was the drive-away depreciation cost. In the linear and SYD models drive-away depreciation accounted for approximately 46% of the total loss in value in the harvester case. In the tractor example, drive-away depreciation accounted for 36.2% of the loss in value of the machine. Assuming drive-away depreciation is incurred in the first year of ownership and separated from the age and use depreciation components, then the ratio of fixed to variable costs is somewhere between1.5:1 and 1.8:1, depending on the model.
The drive-away component of depreciation raises some questions concerning the implications of depreciation on farm management and investment decisions. If drive-away depreciation is incurred as a separate component within the calculation of net farm income in the year it is incurred the impact of NFI and other financial indicators would be significant. In the example used in this study, the drive-away component of the linear model is $44 729 or $65 185 when including brand effects. The former value is $9453 higher than the average total annual depreciation cost, when this component is incurred in the first year of ownership it would reduce NFI by this amount. This reduction in NFI could then affect the timing of investments in capital equipment as a producer would need to time capital purchases to coincide with years of higher NFI to reduce the impact of the higher depreciation charge on profit measures of the farm business.
Conclusions
The objectives in this paper were: to estimate depreciation functions for Australian farm machinery; to determine if any of the functional forms were fitted the data better than the others utilized; and to determine whether machinery depreciation was a fixed or variable cost or a combination of both. In the current study, although the Box-Cox transform model fitted better in the harvester data and was second best fit for the tractor data, based on adjusted R2 and log-likelihood statistics, the overall fit of these models was no better than other simpler forms. T his is in contrast to the results of Wu and Perry (2004). Also, the fit of individual parameters in both Box-Cox models was poor with relatively few significant parameters. However, the results of the current study are consistent with the suggestion of Wu and Perry (2004) that the DSQR or SYD models are reasonable alternatives for the Box-Cox model, with one or both being not significantly different from the Box-Cox model in both data sets.
There is one problem that arises from using the more complex models, such as the DSQR or even the sum of years, and that is the calculation of annual depreciation costs due to usage and age, due to the interaction of these two factors on the remaining value of the harvester or tractor. When calculating annual use and age depreciation costs the simpler models are easier to manipulate to determine these costs. Given the poor fit of individual parameters in the BCT model and that there is no significant difference between the BCT model and more simpler models such as the linear, SQR or the DSQR, it is suggested that depreciation be calculated using one of these simpler models. Because of the complexity of the BCT function, Wu and Perry (2004) suggested and estimated a series of reduced form double-square-root models. However, in the current study either the linear or SQR models would be appropriate to use as both are comparable to the BCT model in terms of adjusted R2 and likelihood ratio tests.
Given that both age and use affect depreciation; when calculating the relative profitability of crops or other enterprises it is possible to assign a value to the variable or usage component of the piece of machinery to an enterprise based on the rate of use and the depreciation cost. This value is then used in the estimation of the gross margin for the enterprise and allows a producer to compare enterprises on the actual usage of machinery for that enterprise. Drive away and age-related depreciation are entered directly into the calculation of net farm income and should not be included in gross margin analysis.
Based on the results of this research it would be reasonable to conclude that the major component of depreciation is age related, but that it is not the sole component of depreciation. Usage-caused depreciation contributes to the costs of machinery ownership. However, two factors, drive away depreciation, or the loss in value from purchase of machinery, and brand effects are also significant costs of machinery ownership that are generally ignored in the calculation of depreciation costs. Therefore, machinery depreciation is both a fixed and variable cost.
References
ABARE, (2003). Australian Commodity Statistics 2002. Australian Bureau of Agricultural and Resource Economics, Canberra.
ABARE, (2004). Australian Commodities: Outlook 2004. Australian Bureau of Agricultural and Resource Economics, Canberra.
Ackerlof, G. (1970) 'The market for lemons: quality uncertainty and the market mechanism.' Quarterly Journal of Economics, Aug, 488-500.
Anon, (2004). ‘Guide to header costs’ NSW Agriculture Farm Enterprise Budget, Available from URL: http://www.agric.nsw.gov.au/reader/machine+water/header-2004.pdf?MIvalObj=1395&doctype=document&MItypeObj=application/pdf&name=/header-2004.pdf. [Accessed 20 October 2004]
Cross, T. L. and Perry, G. M. (1995). ‘Depreciation patterns for agricultural machinery.’ American Journal of Agricultural Economics, 77, 194-204.
Dumler, T. J., Burton, R. O. and Kastens, T. L. (2000). ‘Use of alternative depreciation methods to estimate farm tractor values.’ Paper presented to the annual meeting of the American Agricultural Economics Association, Tampa.
Greene, W. H, (1993). Econometric Analysis. Macmillan Publishing Co., New York.
Harris, G, (2002). ‘Farm machinery costs for broadacre cropping’ DPI&F Note fs0575, Department of Primary Industries and Fisheries, Queensland. Available from URL: http://www.dpi.qld.gov.au/fieldcrops/10907.html [Accessed October 2004]
Heady, E. O., and Jensen, H. R., (1954). Farm Management Economics. Prentice Hall. Englewood Cliffs.
James, S. C. and Eberle, P. R. (2000). Economic and Business Principles in Farm Planning & Production. Iowa State University Press, Ames.
Judge, G. G., Hill, R. C., Griffiths, W. E., Lütkepohl, H. and Lee, T-C. (1988). Introduction to the Theory and Practice of Econometrics. 2nd edn. John Wiley and Sons, Brisbane.
Kruger, I. R. and Logan, R. A. (1980). ‘Farm study of tractor costs.’ Proceedings of the Agricultural Engineering Conference 30 Sept. – 2 Oct 1980, Geelong, Vic.
Makeham, J. P. and Malcolm, L.R. (1993). The Farming Game Now. Cambridge University Press, Melbourne.
Perry, G. M., Bayaner, A. and Nixon, C. J. (1990). ‘The effect of usage and size on tractor depreciation’ American Journal of Agricultural Economics, 72, 317-325.
Power Farming (various dates) Diverse Media Group, Melbourne.
Reid, D. W., and Bradford, G. L. (1987). ‘A farm firm model of machinery investment decisions.’ American Journal of Agricultural Economics, 69, 64-77.
SAS, (1999). User’s Guide: Statistics, Version 8.01 Edition. SAS Inst., Inc. Cary, NC.
Siemens, J.C. and Bowers, W. 1999, Machinery Management: How to select machinery to fit the needs of farm managers. John Deere Publishing, East Moline.
Unterschultz, J. and Mumey, G. (1996). ‘Reducing investment risk in tractors and combines with improved terminal asset value forecasts’. Canadian Journal of Agricultural Economics, 44, 295-309.
Weersink, A. and Stauber, S. (1988). ‘Optimal replacement interval and depreciation method for a grain combine’. Western Journal of Agricultural Economics, 13, 18-28.
Wu, J. and Perry, G. M. (2004). ‘Estimating farm equipment depreciation: which functional form is best?’ American Journal of Agricultural Economics, 86, 483-491.
Table 1: Summary of data for harvester and tractor models.
|
Harvesters (n = 115) |
Mean |
Std Dev |
Minimum |
Maximum |
|||||
|
Age (years) |
6.25 |
2.76 |
1 |
14 |
|||||
|
Total hours |
1873.03 |
942.29 |
250 |
5 232 |
|||||
|
Average hours per year |
305.81 |
93.49 |
131.63 |
795.80 |
|||||
|
Current value |
$175 826 |
$53 604 |
$70 000 |
$331 818 |
|||||
|
Front widtha |
32 |
3 |
25 |
36 |
|||||
|
Real new list price |
$335 817 |
$39 124 |
$253 009 |
$456 769 |
|||||
|
Remaining value |
0.5181 |
0.1245 |
0.1987 |
0.7895 |
|||||
|
Tractors (n = 68) |
|
|
|
|
|||||
|
Age (years) |
7.26 |
3.50 |
1 |
15 |
|||||
|
Total hours |
4218.72 |
2633.82 |
600 |
13422 |
|||||
|
Average hours per year |
633.99 |
306.90 |
133 |
1500 |
|||||
|
Current value |
$88 668 |
$41 932 |
$24 000 |
$250 000 |
|||||
|
Horsepower |
220.81 |
97.58 |
60 |
425 |
|||||
|
Real new list price |
$171 409 |
$63 617 |
$51 049 |
$326 591 |
|||||
|
Remaining value |
0.5173 |
0.1381 |
0.2463 |
0.8935 |
|||||
a Width is reported in feet as this is how they are marketed due to importation from North America.